Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 7
Para a função cujo gráfico é dado, diga o valor de cada quantidade, se ela existir. Se não existir, explique por quê.
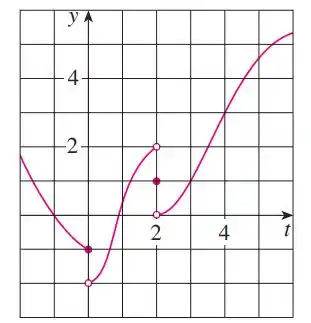
Passo 1
Falaeee, belezinha??? Bom... a questão nos dá o seguinte gráfico:
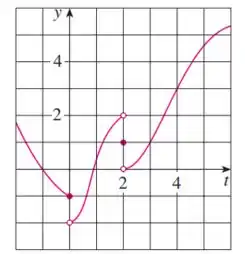
Com isso, queremos determinar o seguinte:
Vamos combinar o seguinte... em cada passo a gente resolve um, belezinha?? 😉
Pois precisamos olhar para o gráfico e tirar as informações que precisamos.
Passo 2
(a)
Quando , e se aproxima de , então, se aproxima de . Logo:
Passo 3
(b)
Quando , e se aproxima de , então, se aproxima de . Logo:
Passo 4
(c)
Os limites laterais são diferentes. Logo:
Não existe
Passo 5
(d)
Quando , e se aproxima de , então, se aproxima de . Logo:
Passo 6
(e)
Quando , e se aproxima de , então, se aproxima de . Logo:
Passo 7
(f)
Os limites laterais são diferentes. Logo:
Não existe
Passo 8
(g)
Pelo gráfico, vemos que a bolinha fechada para está em . Logo:
Passo 9
(h)
Quando se aproxima de , então, se aproxima de . Logo:
Resposta
- não existe
- não existe