Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.2 - Ex. 11d
As funções a seguir definem campos vetoriais sobre . Determinar e fazer os gráficos das curvas onde || é constante.
d)
Passo 1
Belezaaa! Vamos começar outra questão !!
Para calcular || nós podemos usar a equação:
Assumindo que a função é dada como:
Agora que sabemos tudo isso nós podemos começar.
Como é constante:
Na letra (d):
Como é constante:
Podemos substituir:
Removendo a raiz:
Esta é a equação da circunferência, onde k representa o seu raio, e o centro no ponto (2, 4):
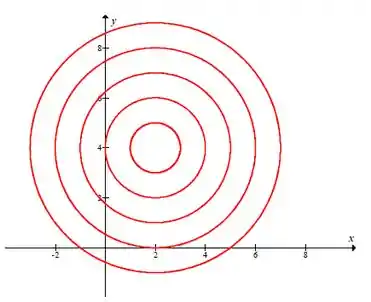
E fiiiim !!!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Encontre uma equação vetorial e equações paramétricas para o segmento de reta que liga P e Q . P - 2,4 , 0 Q = 6 , - 1,2
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce. r t =t 3 ,t 2
Determine a função vetorial que representa a curva obtida pela intersecção das duas superfícies. O cone z = x 2 + y 2 e o plano z = 1 + y .
Encontre uma equação vetorial e equações paramétricas para o segmento de reta que liga P e Q
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce. r t = cos ti - cos t j + sin t k