Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 18

Encontre uma equação vetorial e equações paramétricas para o segmento de reta que liga P e Q

p - 2,4 , 0 , Q ( 6 , - 1,2 )

Passo 1

Fala ai estudioso!

Vamos para mais uma questão?

Essa fala sobre parametrização, então se liga nessa estratégia de resolução!

Para encontrar uma equação vetorial e equações paramétricas para o segmento de reta que liga os pontos quaisquer, podemos usar a forma paramétrica da equação da reta.

Moleza! É só fazer a substituição!

Passo 2

Em 3 dimensões, uma das retas paramétricas que ligam 2 pontos P ( P x , P y , P z ) e Q ( Q x , Q y , Q z ) é igual a:

r t = 1 - t P + t Q

Queremos uma reta paramétrica que liga os seguintes pontos:

P - 2,4 , 0 ,     Q ( 6 , - 1,2 )

Assim, é moleza achar a resposta utilizando a fórmula:

r t = 1 - t . - 2,4 , 0 + t ( 6 , - 1,2 )

r t = - 2 + 2 t , 4 - 4 t , 0 + 6 t , - t , 2 t

Vamos unir as partes literais e não-literal.

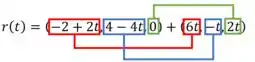
Com isso, teremos.

r t = - 2 + 2 t + 6 t ,   4 - 4 t - t ,   2 t

r t = - 2 + 8 t ,   4 - 5 t ,   2 t

Separando os termos dependentes de t .

r t = - 2 ,   4 ,   0 + t 8 ,   - 5 ,   2

Passo 3

Para encontrarmos as equações paramétricas

Aqui estão as equações paramétricas para cada coordenada:

x t = x P + x Q - x P ⋅ t

y t = y P + y Q - y P ⋅ t

z t = z P + z Q - z P ⋅ t

Substituindo as coordenadas dos pontos P e Q , temos:

x t = - 2 + t 6 - - 2

x ( t ) = - 2 + 8 t

y t = 4 + t - 1 - 4

y t = 4 - 5 t

z t = 0 + t 2 - 0

z t = 2 t

Portanto, as equações paramétricas para o segmento de reta são:

x t = - 2 + 8 t

y t = 4 - 5 t

z t = 2 t

Resposta

Equações vetoriais:

r t = - 2 ,   4 ,   0 + t 8 ,   - 5 ,   2

Equações paramétricas:

x t = - 2 + 8 t

y t = 4 - 5 t

z t = 2 t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize um computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a revelar a verdadeira natureza da curva. r t = t 2 , t - 1 , 5 - t
Utilize o computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a garantir que a visualização é verdadeira. r → t =s e n t , c o s t , t 2
Esboce o gráfico da curva cuja equação vetorial é dada. Identifique com seta a direção na qual o parâmetro cresce r → t = t 4 + 1 , t
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com seta a direção na qual o parâmetro cresce. r → t = s e nti → + s e ntj → + 2 cos ⁡ t k →
Esboce o gráfico da curva plana com a equação vetorial dada.Determine r ' ( t ) .Desenhe o vetor de posição r ( t ) e o vetor tangente r ' t para o valor dado de t . r t = cos ⁡ t , sen ⁡ t ,t = π 4