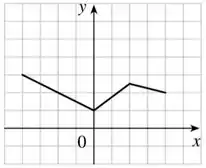
O gráfico de é dado. Esboce os gráficos das seguintes funções:
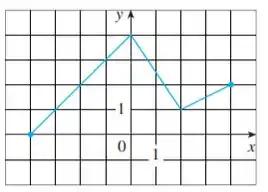
Passo 1
E aí pessoal, tudo beleza? Para resolver essa questão, temos que aplicar o conceito de transformações de funções, tranquilo? Bora começar:
- Nessa aqui, o gráfico de irá vira o de se for deslocado unidades na horizontal, para a esquerda. Toda vez que somamos ou subtraímos no argumento da função, nós vamos deslocar o gráfico na horizontal, fechou? Olha aqui como fica:
- Nessa aqui, a soma (que poderia ser subtração) não ta ocorrendo no lado de dentro, no argumento, mas sim do lado de fora! Nesses casos, a gente desloca tooodo o gráfico na vertical para cima em unidades, aí nós vamos ter o gráfico da nova função :
- Como a gente ta multiplicando por , a gente vai deformar ele na vertical, expandido por um fator . As multiplicações e divisões sempre vão comprimir ou expandir o gráfico de alguma forma, lembra disso! Olha como vai ficar esse:
- Esse aqui é o nosso útlimo item! Vamos ter três processos para fazer com . Você pode fazer em qualquer ordem quando estiver desenhando, ok? ;)
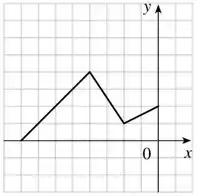
Passo 2
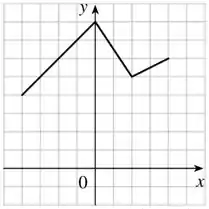
Passo 3
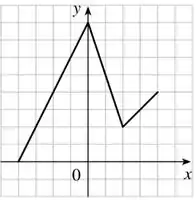
Passo 4
Primeiro, temos que comprimir o gráfico na vertical por um fator (que é o número pelo qual está sendo dividido). O próximo passo é refletir o gráfico com relação ao eixo , ou seja, girar ele em torno desse eixo. Por fim, nós vamos deslocar ele na vertical em unidades, resultando no gráfico abaixo:
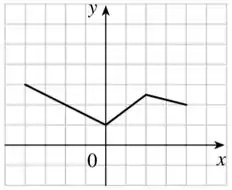
Dá até pra ver que o “pico” dele que ficava em cima do eixo ta de cabeça pra baixo e que o gráfico ta mais espremido na vertical né? Esses são dois indícios das transformações que a gente fez.
Resposta