Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 51
Faça o gráfico da função:
Passo 1
Então galera, primeiramente devemos estabelecer o domínio dessa função. Como a variável está no denominador, sabemos então que a parte de baixo não pode ser zero! Sendo assim, temos:
Descobrimos então que para x = 1 a função não existe! Logo, o domínio será:
Nesse ponto específico, aparece o que a gente chama de assíntota vertical, que é representado como um pontilhado vertical.
Passo 2
Agora que encontramos para que valor de a função tende, devemos nos perguntar também quanto valerá quando for muuuuito grande, ou seja, tendendo ao infinito!
Se fizermos isso, teremos um número dividido por um valor muito grande, então dizemos que isso dá aproximadamente 0. Se liga só!
Passo 3
Tendo em vista os valores encontrados, conseguimos concluir que a função vai tender a 1 verticalmente e vai tender a 0 horizontalmente. Plotando essas informações, teremos:
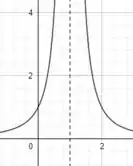
Resposta
O gráfico de é:
