Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 35
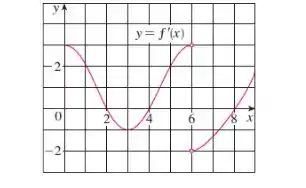
O gráfico da derivada de uma função contínua está ilustrado.
(a) Em que intervalos está crescendo ou decrescendo?
(b) Em que valores de a função tem um mínimo ou máximo local?
(c) Em que intervalos é côncava para cima ou para baixo?
(d) Diga as coordenadas dos pontos de inflexão.
(e) Supondo que , esboce o gráfico de .
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão dá pra gente o gráfico da derivada de uma função . Esse gráfico é o seguinte.
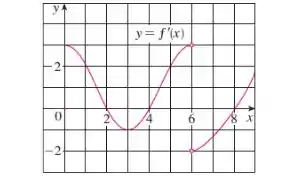
E pede pra gente responder aos seguintes itens. Mas antes de ver o que a questão está querendo, vamos relembrar algumas informações importantes.
A derivada de uma função é entendida como a inclinação da reta tangente a curva do gráfico da função.
Sabendo disso, podemos pensar que quanto mais positiva a derivada estiver, mais rapidamente a função original estará crescendo.
Assim:
Sabendo disso, teremos que dizer:
(a) Em que intervalos está crescendo ou decrescendo?
Para isso, bastar observarmos onde o gráfico da derivada é positivo ( estará crescendo) e onde o gráfico da derivada é negativo ( estará decrescendo).
(b) Em que valores de a função tem um mínimo ou máximo local?
Isso vai acontecer quando o gráfico da derivada estiver no zero.
(c) Em que intervalos é côncava para cima ou para baixo?
Pra isso temos que pensar na derivada de segunda ordem . Sendo a inclinação da reta tangente ao gráfico da primeira derivada.
Assim:
(d) Diga as coordenadas dos pontos de inflexão.
O ponto de inflexão acontece onde a derivada de segunda ordem for igual a zero. Assim:
Que serão os pontos de máximo ou mínimo do gráfico da derivada da função
E por fim, no item
(e) Supondo que , esboce o gráfico de .
Passo 2
Item a:
O sinal da derivada indica se função está crescendo (derivada positiva) ou decrescendo (derivada negativa).
Podemos observar no gráfico que nos intervalos
, e
Temos
e nos intervalos
e
Temos
então:
é crescente nos intervalos , e e decrescente nos intervalos e .
Passo 3
Item b:
Se passa de positiva para negativa temos uma máximo local e se passa de negativo para positivo temos um mínimo local.
Então, temos máximo local em
e
e temos mínimo local em
e
Passo 4
Item c:
A concavidade de uma função é dada pelo sinal da derivada segunda. Se a derivada segunda for negativa, a concavidade da função é voltada para baixo e se for positiva a concavidade é voltada para cima.
Como a derivada segunda aponta o crescimento e decrescimento da derivada primeira, então quando a derivada segunda for negativa, a derivada primeira será decrescente e caso seja positiva, a derivara primeira será crescente. Portando, podemos ver pelo gráfico que é crescente nos intervalos e e é decrescente no intervalo , então:
possui concavidade para cima nos intervalos e e concavidade para baixo no intervalo .
Passo 5
Item d:
Os pontos de inflexão são aqueles em que a derivada segunda é nula, ou seja, a concavidade muda de sinal, então:
O único ponto de inflexão é .
Passo 6
Item e:
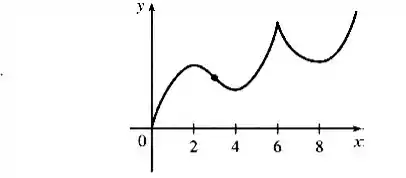
Se , o gráfico de passa pela origem, então de acordo com as informações levantadas nos itens de (a) a (d) temos o seguinte gráfico:
Resposta
(a) é crescente nos intervalos , e e decrescente nos intervalos e .
(b) Temos máximo local em e e temos mínimo local em e .
(c) possui concavidade para cima nos intervalos e e concavidade para baixo no intervalo .
(d) O único ponto de inflexão é .
(e)
