Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.2 - Ex. 33
O gráfico da figura a seguir mostra a variação percentual média anual,
do produto interno bruto (PIB) norte-americano entre os anos 1983-1988. Represente graficamente (onde for definido).
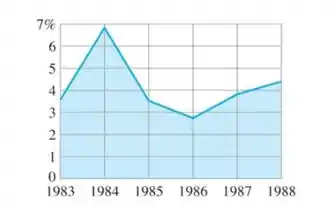
Passo 1
Primeiro, devemos entender em quais pontos a derivada é definida. Quando uma função é afim, a sua derivada é igual ao seu coeficiente angular; logo, se temos uma função definida por partes, onde todas as partes são afim, não há como definir a derivada em um ponto comum a duas pares.
Passo 2
Em seguida, devemos notar que a função é definida por 5 segmentos de reta, logo, o gráfico da derivada também deve conter 5 segmentos de reta.
Como a derivada de uma função afim é o próprio coeficiente angular da função, temos que o gráfico de é composto por segmentos constantes.
Passo 3
Para saber o valor da derivada em cada segmento, basta calcular o coeficiente angular de cada parte da função.
Segmento 1:
Segmento 2:
Segmento 3:
Segmento 4:
Segmento 5:
Passo 4
Por fim, basta traçar o segmentos de reta da seguinte forma:
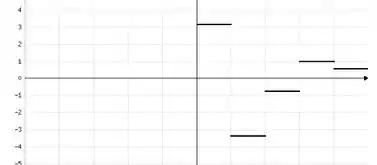
Resposta
Ei, a resposta está no passo a passo :)