Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 33
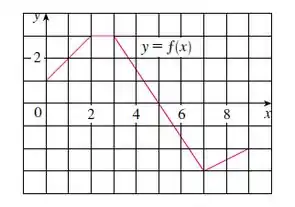
O gráfico de está mostrado. Calcule cada integral interpretando-a em termos das áreas.
a)
b)
c)
d)
Passo 1
Eaeee, belezinha??? Bom... o enunciado nos dá o seguinte gráfico de uma função :
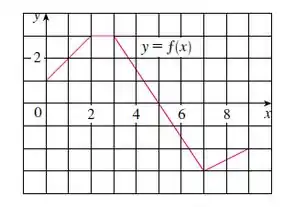
E quer que calculemos as seguintes integrais:
a)
b)
c)
d)
Para isso, devemos entender que a integral é a área sob a curva e que uma integral de uma função é dada por:
Onde é o intervalo de integração!!
Agora bora lá!! 😉
Passo 2
Para calcular as integrais vamos ver as áreas formadas na figura entre os limite de integraçãode cada integral, e calcular essa área, simples.
a) Aqui temos que os limites de integração são e , e temos então um trapézio, com base maior , base menor e altura , só calcular a área do trapézio, e teremos o valor da integral:
Passo 3
b) Aqui temos que os limites de integração são e , e vamos dividir a figura em três partes, para ficar simples de calcular as áreas, em um trapézio, com base maior , base menor e altura , um retângulo, com base e altura e um triângulo com base e altura , agora é só calcular as somas dessas áreas, e teremos o valor da integral:
Passo 4
c) Aqui temos que os limites de integração são e , e temos então um triângulo, com base e altura , porém aqui a figura está abaixo do eixo , então a área aqui é negativa, temos que colocar um sinal de menos e calcular a área do triângulo, assim teremos o valor da integral:
Passo 5
d) Aqui temos que os limites de integração são e, e pelas propriedades das integrais , sabemos que:
A área abaixo da curva de até é a de um trapézio, com base maior , base menor e altura , mas como está abaixo do eixo , assumiremos seu valor negativo.
Logo,
Entendeu direitinho?? Responde aee 😉
Resposta
a)
b)
c)
d)