Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 6.13 - Ex. 14
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas.
Passo 1
Devemos começar as questões que pedem para calcularmos a área de uma região sempre pelo esboço dessa região. Se não esboçarmos ele, não conseguiremos compreender a integral que devemos calcular. Sendo assim, vejamos a região abaixo:
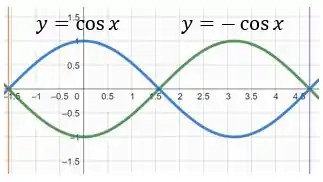
Percebam que temos duas regiões limitadas por ambas às curvas. Para a região de , a curva está acima da curva . Já no caso da região , temos o contrário. Portanto, precisamos levar este fato em consideração na hora de montarmos a nossa integral. Desta forma, temos:
Podemos ir mais além. Como ambas as regiões são iguais, podemos transformar as nossas integrais em apenas 1. Basta fazermos:
Passo 2
Agora que conseguimos escrever a integral que nos dá a área, só nos resta calculá-la. Portanto, temos:
Portanto, a área da nossa região é: