Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 13c
Um gráfico que seja grande o suficiente para mostrar o comportamento global de uma função pode deixar de revelar aspectos locais importantes. O gráfico de é um desses casos.
c. Amplie o gráfico para encontrar uma janela de visualização que mostre a presença de valores extremos locais em e .
Passo 1
Agora, ampliando o gráfico da função na parte desejada:
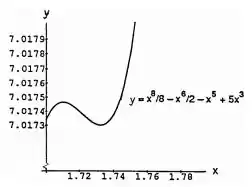
Portanto, é possível observar que existem de fato extremos locais nos pontos citados ( e ).
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada