Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 1
Determinar a partir do gráfico se a função possui algum valor extremo absoluto em . Em seguida, justifique sua resposta com base no Teorema 1.
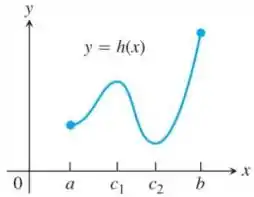
Passo 1
Observando o gráfico da função apresentada, pode-se observar que tal função possui mínimo absoluto no ponto e máximo absoluto em .
Passo 2
Tal fato pode ser justificado através do Teorema 1 pelo fato de que a função é contínua em todo o intervalo .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Uma fazenda de gado permite 20 novilhos por 50m 2 de pasto. O peso médio de seus novilhos no mercado é de 900k g . Estimativas do Departamento de Agricultura (EUA) indicam que o peso médio ficará redu
Qual a menor inclinação possível para uma reta tangente à equação y = x 3 - 3 x 2 + 5 x ?
Mostre que f x = sec x + c o s s e cx tem um valor mínimo, mas nenhum valor máximo no intervalo 0 , π 2 . Encontre o valor mínimo da parte (a).
Um trapézio é inscrito em um semicírculo com raio 2 , de forma que um lado está sobre o diâmetro (Figura Ex-47). Encontre a maior área possível para o trapézio. [Sugestão: Expresse os lados do trapézi
Um canal de drenagem deve ser feito de tal forma que a secção transversal é um trapézio com os lados igualmente inclinados (Figura Ex-48). Se os lados e a base tiverem um comprimento de 5m , como esco