Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 69
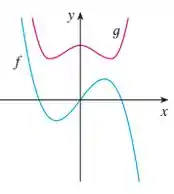
Os gráficos de e de são mostrados a seguir. Verifique se cada função é par, ímpar, ou nem ímpar nem par. Explique seu raciocínio.
Passo 1
Fala aí! tudo certinho? 😉
Nesse problema foi dado um gráfico de duas funções e nosso objetivo é determinar se essas funções são pares, ímpares ou nenhuma das duas.
Lembra do que a gente precisa pra analisar o gráfico?
Pra função ser par, ela precisa ser simétrica em relação ao eixo .
já pra ser ímpar, precisa ser simétrica em relação à origem.
Bora lá! 😉
Passo 2
Primeiramente vamos analisar a função ...
Perceba que o lado negativo de tem exatamente o mesmo formato da parte positiva, porém refletida em relação ao eixo .
Portanto, por conta dessas características, podemos afirmar que é uma função ímpar.
Já está refletida em relação ao eixo .
Apenas por essa característica, podemos afirmar que é uma função par.
O que achou? Responde Aí! 😊
Resposta
é ímpar e é par.