Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 70
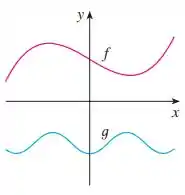
Os gráficos de e de são mostrados a seguir. Verifique se cada função é par, ímpar, ou nem ímpar nem par. Explique seu raciocínio.
Passo 1
Fala aí, pessoal! Tudo certinho? 😉
Nesse problema temos dois gráficos de funções e nosso objetivo é classifica-las como par, impar ou nenhuma das duas...
Lembra do que a gente precisa pra analisar o gráfico? Pra função ser par, ela precisa ser simétrica em relação ao eixo ¸e pra ser ímpar, precisa ser simétrica em relação à origem, como se a estivesse girando ele em .
Marca aí! 😉
Passo 2
Se colocarmos um espelho no eixo e olharmos para os reflexos da função vamos observar que o que será refletido será diferente do que existe de fato, ou seja
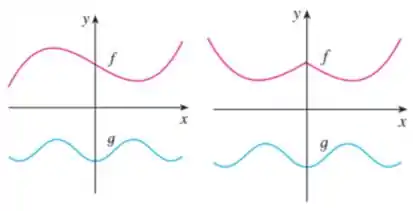
Portanto podemos afirmar que a função não é par.
O contrário da função que quando espelhada em relação ao eixo o que está refletido é igual o que está de fato no gráfico, logo é uma função par.
Legal, não é? 😁
Passo 3
Agora podemos usar uma característica interessante para provar que e não são ímpares...
Perceba que tanto quanto são funções contínuas.
Nesse caso, para uma função continua ser considerada ímpar, ela deve necessariamente passar pela origem.
Como nem e nem passam pela origem, podemos dizer que ambas não são funções ímpares!
E aí! Entendeu tudo? Responde Aí! 😉
Resposta
não é nem uma nem outra, e é par.