Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.7 - Ex. 35
Ache as assíntotas horizontal e vertical do gráfico de , determinando o seguinte:
Os extremos relativos de ;
Os pontos de inflexão do gráfico de ;
Os intervalos em que é crescente
Os intervalos em que é decrescente;
Onde o gráfico é côncavo para cima;
Onde o gráfico é côncavo para baixo;
A inclinação de qualquer tangente de inflexão;
As assíntotas horizontal, vertical e oblíqua, se existirem
Passo 1
Vamos começar olharando as assíntotas:
Vamos começar pela assíntota horizontal.
Assíntota horizontal: fazer o limite no infinito. Ou seja,
Com esse intervalo que ele fechou, não vai existir assíntota, porque a função não vai para o infinito.
Então ele não tem assíntota horizontal, nem as oblíquoas.
Passo 2
Vamos para as verticais. Para isso, temos que procurar algum valor de que faça o limite ir para . Normalmente procuramos quando o denominador da fração for , a tangente é uam fração
Então quando o coseno for , são as possíveis assíntotas verticiais.
Mas aqui vai a minha dica para vocês, no caso da tangente as assíntotas verticais são:
E a tangente vai para pela esquerda e pela direita
Mas aqui temos
Então as assíntotas serão:
Mas o intervalo vai de até . Vamos ter e
E
Passo 3
Vamos aos extremos e os intervalos de crescimento e decrescimento. Para isso temos que analisar o sinal de .
Lembrando que ele limitou o entre e .
Isso é a secante ao quadrado, ou seja, é um termo ao quadrado, vai ser sempre positivo.
A função é crescente se e decrescente se , então:
Passo 4
Agora vamos ver os extremos. Pelo teste da primeira derivada, teremos máximo quando a função vai de crescente para decrescente, e mínimo quando a função for de decrescente para crescente.
Como a função é sempre crescente, ela não vai ter extremo.
Passo 5
Vamos agora para a concavidade e os pontos de inflexão. A função é côncava para cima se e côncava para baixo se .
O sinal vai depender so de , porque é um termo ao quadrado.
A vai ser positivo entre e , e vai ser negativa em e , somando nos extremos também, com sendo inteiro.
Mas aali temo e não , vamos fazer:
Arrumando isso, ao multiplicar o intervalo por , vamso ter
Vamso pegar primeiro
Temos que pegsar a primeira parte só porque o intervalo é até .
Vamos para o outro lado com
Arrumando isso
Vamos pegar só o segundo, porque o intervalo começa em
Os intervalos que ficaram foram:
Vams ter
Então:
Isso nos diz que em:
muda de concavidade, então é um ponto de inflexão.
Passo 6
Para terminar vamos ao esboço. Para isso, precisamos juntar todas as informações.
- Assíntotas verticais: , x
- , ponto de inflexão
- Tangente de inflexão:
- Assíntotas verticais: , x
- , ponto de inflexão
- Tangente de inflexão:
Ele pede també a tangente de inflexão que nada mais é que a derivada no ponto de inflexão
Vamos para o gráfico, ele vai ficar assim:
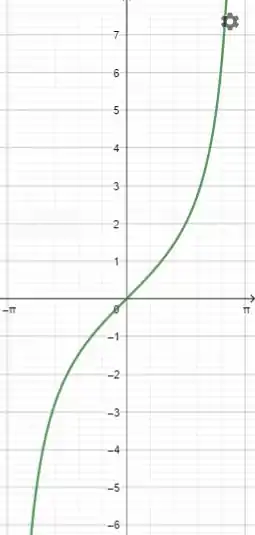
Resposta
Ele pede també a tangente de inflexão que nada mais é que a derivada no ponto de inflexão
Vamos para o gráfico, ele vai ficar assim:
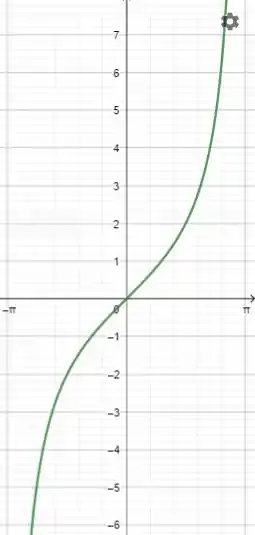
Resposta
Ei, a resposta está no passo a passo :)