Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 62
Uma janela normanda tem o formato de um retângulo em cima do qual se coloca um semicírculo. Se o perímetro da janela for de m, expresse a área da janela como uma função de sua largura .
Passo 1
Eaee, belezinha??
Bom... a questão quer que encontremos uma expressão da área de uma janela em função de sua largura .
Como dado, a questão nos diz que a janela tem o formato de um retângulo em cima do qual se coloca um semicírculo.
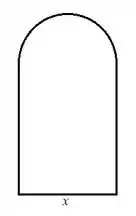
Além disso, o perímetro da janela é de m.
Para resolvermos isso, temos que arranjar uma forma de relacionarmos o perímetro com a área da janela, de forma que a variável independe.
E aí?? Bora lá?? 😉
Passo 2
Note que, se a largura da janela é , significa que o diâmetro do semicírculo também é .
Opa, então, temos que o raio dele é .
Chamando de o comprimento da parte retangular da janela e sabendo que o comprimento de metade de uma circunferência é (onde é o raio dela), temos que o perímetro dela será:
Tranquilo até aqui? 😎
Passo 3
A área da janela, será a soma das áreas das partes representadas pelo semicírculo e pelo retângulo.
Como a área do semicírculo é , temos que:
Substituindo , temos:
Entendeu direitinho?? Responde Aí 😉
