Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 10
10. Determine se a curva é o gráfico de uma função de . Se o for, determine o domínio e a imagem da função.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema nosso objetivo é determinar se o gráfico dado é definido por alguma função se e se for queremos determinar a domínio e a imagem dessa função.
Parece complicado? 🤔
Uma função de é uma regra que associa cada valor de a um único valor de , chamado de imagem.
Podemos relacionar o domínio e a imagem de uma função como as possíveis entradas e saídas, respectivamente, da função.
O domínio são as possíveis entradas, ou seja, os possíveis valores que pode assumir para a função ser definida.
Já a imagem são os possíveis valores de saída, ou seja, os possíveis valores que a função pode resultar.
Bora lá! 👀
Passo 2
O gráfico é dado por
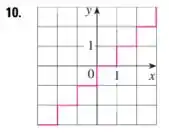
A primeira coisa que podemos perceber é que esse gráfico representa uma escadinha com degraus unitários.
Perceba que em (números inteiros) o gráfico é uma linha vertical.
Dessa forma, podemos afirmar que esse gráfico não representa uma função já que para um valor de , temos diversas imagens em .
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
