Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.2 - Ex. 10
- Na janela retangular por , faça o gráfico da função e de sua reta secante que passa pelos pontos e . Use o gráfico para estimar as coordenadas dos pontos onde a reta tangente é paralela à reta secante.
- Encontre os valores exatos dos números que satisfaçam à conclusão do Teorema do Valor Médio para o intervalo e compare com sua resposta da parte (a).
Passo 1
Faaala meus queridos...Nessa questão vamos usar um recurso gráfico para plotar o gráfico da função
Então, vamos traçar a reta secante que passa pelos pontos e
Por fim, vamos olhar no gráfico quais são os pontos em que a reta tangente possui a mesma inclinação que a reta secante.De acordo com o Teorema do Valor Médio, deve haver pelo menos um ponto onde isso acontece.
Por fim, na letra b), vamos encontrar analiticamente quais são esses pontos. Para isso, vamos encontrar a inclinação de reta secante, fazendo:
E por fim, vamos encontrar quais são os pontos da função que possuem derivada igual a inclinação que encontramos.
Passo 2
Bom, vamos lá, plotando o gráfico na janela gráfica pedida, temos o seguinte:
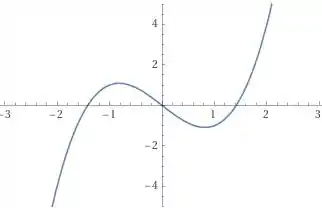
Agora traçando a reta secante entre os pontos e
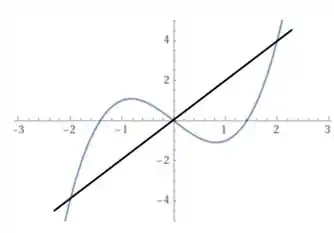
Agora, de forma visual, vamos procurar quais são os pontos que possuem reta tangente com inclinação igual a da reta secante que traçamos.
Esses pontos onde as retas tangentes possuem inclinação igual a da secante, são aproximadamente, olhando no gráfico
Passo 3
Agora para a letra b) vamos encontrar esses pontos analiticamente.
O primeiro passo aqui é encontrar a inclinação da reta secante.
Usando os valores dos pontos dados, temos:
Agora, devemos procurar pelos pontos de dentro do intervalo que possuem derivada igual a 2 (isso indica que esses pontos possuem reta tangente com inclinação ).
O primeiro passo é encontrar a derivada da função:
Agora encontrar os pontos em que essa derivada vale .
Aplicando a raiz quadrada em ambos os lados e não esquecendo do , temos:
Portanto, analiticamente, encontramos que os valores de são:
Resposta
a)
b)