Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.8 - Ex. 9
(a) Encontre um intervalo no qual
Satisfaz as hipóteses do Teorema de Rolle.
(b) Gere o gráfico de e use-o para fazer estimativas de todos os valores de obtidos em (a) que satisfazem a conclusão do Teorema de Rolle.
(c) Use o Método de Newton para melhoras as estimativas obtidas em (b).
Passo 1
(a) Bom, para acharmos um intervalo, temos que satisfazer as hipóteses do teorema em que a função deve ser contínua no intervalo fechado e diferenciável no intervalo aberto. Nossa função é contínua para todo o conjunto dos reais e também é diferenciável no mesmo conjunto, já que .
Então, vamos só encontrar dois pontos em que a função possua o mesmo valor! Já que, como ela satisfaz as hipóteses em qualquer valor de , podemos pegar qualquer intervalo nessa função.
Vamos testar o valor de :
Se a gente pegar :
Hm, cresceu demais, vamos ver os valores menores que , então. :
:
Opa, e não é que ? Então, esse pode ser nosso intervalo:
Passo 2
(b) Aqui, queremos estimar onde a derivada é zero, usando o gráfico dela.
O gráfico da derivada é:
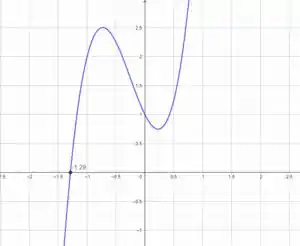
Dá para ver ali que a derivada é zero em, aproximadamente, . Então, esse é o nosso cara!
Passo 3
(c) Então, vamos usar o método de Newton para chegar em um resultado melhor que o da (b).
Queremos que:
E vemos, no gráfico, que esse valor está próximo de , logo ele será nosso . Vamos achar os próximos valores e ver para onde converge:
Continuando o método:
Opa, devido à repetição dos valores, vemos que é uma aproximação para o valor que queremos.
Resposta
(a)
(b)
(c)