Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.5 - Ex. 18
Um lago é formado quando a água se acumula em uma depressão cônica de raio e profundidade . Suponha que a água flui para dentro a uma taxa constante e é perdida por evaporação a uma taxa proporcional à área de superfície.
(a) Mostre que o volume de água no lago em qualquer instante satifaz a equação diferencial
Em que é o coeficiente de evaporação.
(b) Encontre a profundidade de equilíbrio de água no lago. Esse equilíbrio é assintoticamente estável?
(c) Encontre uma condição que tem que ser safisfeita para o lago não transbordar.
Passo 1
Como sugerido no item (a), nosso primeiro passo tem que ser resolvendo nossa equação diferencial. Assim tome o passo a baixo.
Passo 2
(a) Vamos olhar primeiro para nosso lago
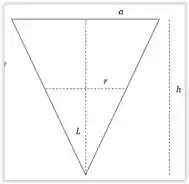
Assim por simetris de triangulo, temos que, quando a água tiver a uma altura , temos que
Desta forma temos que o volume de água a esse nível é dado por
Pelo enunciado temos que
Passo 3
(b) Para encontrarmos a profundidade de equilíbrio, devemos analisar quando a derivada é nula, ou seja
Usando a relação que obtivemos no passo anterior, temos
Passo 4
(c) temos que quando precisamos que sempre , ou seja
O que implica que
Mas lembrando, quando temos que assim
Assim nosso condição é que
Resposta
(b)