Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 48
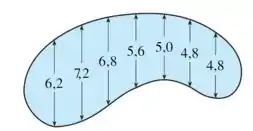
As larguras (em metros) de uma piscina com o formato de rim foram medidas a intervalos de metros, como indicado na figura. Use a regra do ponto médio para estimar a área da piscina.
Passo 1
Opa, bora resolver esse problema! Temos uma piscina com o seguinte formato:
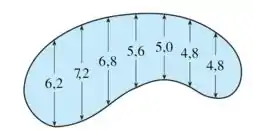
Devemos usar a regra do ponto médio pra estimar a área total dessa piscina:
Onde
Temos intevalos, como queremos o ponto médio de cada uma, teremos e cada intervalo tem então:
Passo 2
Com isso, podemos então escrever a seguinte integral:
Calculando:
Prontinho!
Resposta
Exercícios de Livros Relacionados
Determine as áreas das regiões compreendidas entre as retas e as curvas y = 7 - 2 x 2 E y = x 2 + 4
Determine as áreas das regiões compreendidas entre as retas e as curvas y = x 2 - 2 x E y = x
Determine as áreas das regiões compreendidas entre as retas e as curvas y = x 2 E y = - x 2 + 4 x
Desenhe a curva dada (coordenadas polares ). d )ρ = 2
Desenhe a curva dada (coordenadas polares ). b ) ρ cos θ = 1 , - π 2θπ 2