Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 56
Encontre a área da região limitada pela parábola , pela reta tangente a essa parábola em e pelo eixo .
Passo 1
Bom, galera, nesse exercício queremos calcular a área da região entre a parábola e sua reta tangente.
Sabemos que a reta tangente dessa parábola passa no ponto e que ela toca o eixo .
Precisamos encontrar a função da reta tangente:
O coeficiente angular, , aqui é nada mais nada menos do que a derivada da parábola no ponto dado:
Agora determinamos a equação da reta fazendo:
Substituindo o ponto
Passo 2
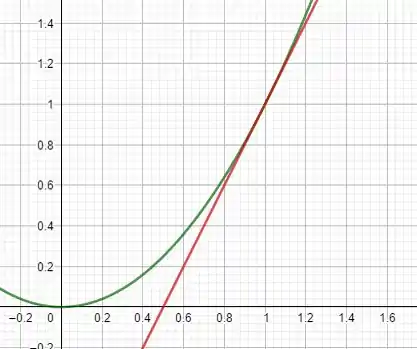
Agora que conhecemos as duas curvas podemos esboçar o gráfico:
L
embrando que nossa área está limitada pelo eixo também!! Podemos então calcular a área da seguinte maneira:
Teremos, de 0 até 1/2, apenas a parábola:
E, de 1/2 até 1, temos a parábola menos a reta:
Por que deixei esse sem somar? Então, porque nós temos que a área total será a soma das duas áreas que encontramos! Então:
E olha como eles se cortam ali:
Prontinho!!