Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 45
Use um sistema de computação algébrica para encontrar a área exata da região delimitada pelas curvas e .
Passo 1
E aí, galerinha! 😊
Nesse exercício iremos utilizar um sistema de computação algébrica para calcular a área entre as curvas apresentadas, e .
Parece complicado? 😐
Passo 2
Graficamente podemos visualizar melhor a região de interesse
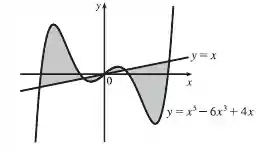
Podemos escrever a seguinte integral
Utilizando um sistema de computação algébrica, chegamos no seguinte valor
Achou tranquilo? Responde Aí! 😉
Resposta
Exercícios de Livros Relacionados
Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas
57- Área de superfície Determine a área da superfície gerada pela rotação da curva y = x 2 + 2 , 0 ≤ x ≤ 2 , em torno do eixo x .
Determine as áreas das regiões compreendidas entre as retas e as curvas nos Exercícios 73-80.75. y 2 - 4 x = 4e4 x - y = 16
Determine as áreas das regiões compreendidas entre as curvas nos Exercícios 81-84.84. x + y 2 = 3e4 x + y 2 = 0