Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.3 - Ex. 63
A Lei do Paralelogramo afirma que
- De uma interpretação geométrica para a Lei do Paralelogramo.
- Demonstre a Lei do Paralelogramo. [Sugestão: Use o fato de que e utilizr a Propriedade 3 do produto escalar].
Passo 1
Bom, se isso é uma lei do PARALOLOGRAMO, tem a ver com paralelogramo. Então vamos pensar em e como lados de um paralelogramo.
Sabemos que o paralelogramo tem lados iguais e paralelos dois a dois. Então se pensarmos nesses lados como vetores para formar um poligno fechado, podemos dizer que se um lado é seu paralelo é e se um lado é , seu parabelo é
Com isso, podemos também formar duas diagonais, que seriam dadas pelos vetores
Geometricamente temos:
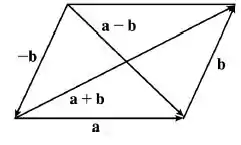
A lei diz que a soma dos quadados dos tamanhos dos vetores das diagonais é igual a soma dos quadrados dos quatro lados do paralelogramo.
Passo 2
Vamos começar usando a sugestão dele:
Além disso,
Somando as duas equações:
Resposta
A lei diz que a soma dos quadados dos tamanhos dos vetores das diagonais é igual a soma dos quadrados dos quatro lados do paralelogramo.