A leitura do odômetro de uma motocicleta em intervalos de 12 segundos é mostrada na tabela a seguir.
![]()
- Estime a distância percorrida pela motocicleta durante esse período, usando a velocidade no começo dos intervalos de tempo.
- Dê outra estimativa usando a velocidade no fim dos intervalos de tempo.
- As estimativas feitas nas partes (a) e (b) são estimativas superior e inferior? Explique.
Passo 1
E aí, beleza? Bora entender essa questão juntos 😊?
O enunciado pede para estimarmos a distância percorrida pela motocicleta durante um determinado período de tempo, considerando uma determinada velocidade em cada item.
Antes de resolvermos a questão, vamos listar as informações que já sabemos:
- Seis instantes de tempo onde a velocidade da motocicleta foi medida. Dando origem a cinco intervalos de tempo.
- A velocidade da motocicleta (em pés/s) no início e no fim de cada intervalo de tempo.
Talvez não esteja tão claro qual é a velocidade no fim de cada intervalo de tempo. Mas pensa aqui comigo, entre duas marcações de tempo sempre terá um intervalo de tempo, certo? Assim, a velocidade no fim de um intervalo deve ser a velocidade no início do próximo.
Para facilitar o trabalho na hora de fazermos as contas, bora organizar essas informações em uma tabela.

Beleza, mas como vamos resolver isso?
Imagina que a velocidade permanecesse constante igual a durante todo o período de tempo , então a distância percorrida seria simplesmente
Mas esse não é o nosso caso, certo?
Mas a velocidade dentro de um intervalo de tempo pequeno não pode variar muito. Por causa disso, vamos assumir que dentro de cada intervalo, a velocidade é mantida constante.
Mas para velocidade constante já sabemos como calcular. Então, assumindo uma velocidade constante em cada intervalo, vamos ter que a distância será:
onde a velocidade vai depender do item (a) ou (b), mas que já deixamos mastigadinho na tabela anterior 😍. Não esquece da unidade de medida, combinado? Como a de é e a de é , então a de será
Além da distância a ser calculada nos itens (a) e (b), precisamos dizer se as estimativas encontradas em cada item são superior ou inferior. Mas por qual motivo estamos encontrando estimativas, e não as distâncias em si?
Bem, estamos fazendo uma simplificação ao assumirmos que a velocidade é constante em cada intervalo. Não sabemos como a função velocidade é, de fato. Logo, não sabemos o valor exato da distância, mas temos como encontrar uma estimativa.
Passo 2
Item (a): Aqui, a velocidade é a do início de cada intervalo.
Vamos calcular as distâncias, uma para cada intervalo de tempo, usando os valores da segunda coluna da tabela do Passo 1. Vamos lá!
Para cada intervalo , e , temos:
Para a estimativa da distância total, vamos somar todas as distâncias, ou seja,
e vamos substituir cada uma delas pela fórmula anterior. O número aparece multiplicando a velocidade em todos os termos da soma, então vamos colocar ele em evidência e obter:
Agora é só substituir pelos valores dados na segunda coluna da tabela e realizar as operações matemáticas, quer ver?
Passo 3
Item (b): Aqui, a velocidade é a do fim de cada intervalo. Logo, para cada intervalo de tempo, vamos usar os valores da terceira coluna da tabela do Passo 1.
Novamente,
Agora vai mudar um pouquinho, pois precisamos usar a velocidade no fim do intervalo de tempo. Mas, para isso, só precisamos substituir pelos valores dados na terceira coluna da tabela e realizar as operações matemáticas:
Passo 4
Item (c): Para analizarmos se as estimativas encontradas são superiores ou inferiores, vamos tentar dar um significado para os valores de distância que calculamos nos Passos 2 e 3.
Podemos pensar na fórmula
como sendo o cálculo da área de um retângulo de lados e .
Além disso, podemos marcar os pontos dados nas colunas da tabela do Passo 1, e ligarmos esses pontos para esboçar uma possível curva para a função velocidade. Para cada item da questão, teremos dois cenários:
- a velocidade inicial faz com que a altura de cada retângulo coincida com o valor da função no início do intervalo. (Gráfico a esquerda)
- a velocidade final faz com que a altura de cada retângulo coincida com o valor da função no final do intervalo. (Gráfico a direita)
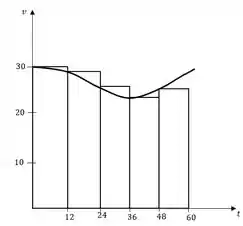
Analisando os gráficos, em ambos os casos há partes nas quais o retângulo passa da curva e partes nas quais ele não passa.
Dessa forma, não conseguimos dizer que as aproximações são superiores ou inferiores, precisaríamos conhecer toda a função , pois isso nos permitiria calcular o valor exato da distância e compararmos com as estimativas encontradas.
Resposta
- .
- .
- Não há como saber se são estimativas encontradas são superiores ou inferiores.