Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.1 - Ex. 1
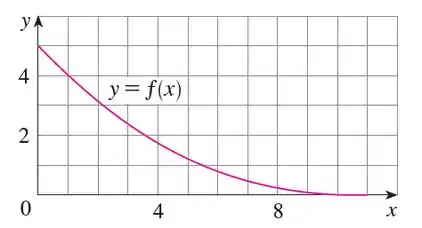
- Ao ler os valores do gráfico dado de , use cinco retângulos para induzir uma estimativa mais baixa e uma estimativa mais alta para a área sob o gráfico dado de de a . Em cada caso, esboce os retângulos que você usar.
- Encontre novas estimativas usando dez retângulos em cada caso.
Passo 1
Oie, tudo bem?
Vamos resolver essa atividade. A gente tem o gráfico:
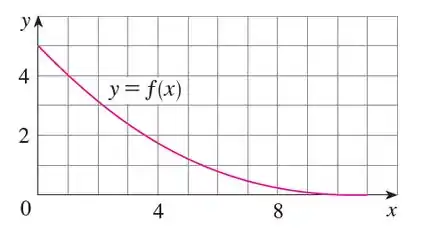
E a gente quer encontrar a área abaixo desse gráfico. Mas queremos encontrar a área aproximada, então para isso o que iremos fazer é criar diversos mini retângulos em toda região abaixo do gráfico, e assim aproximarmos a área.
Iremos fazer isso utilizando de inicio retangulos, e depois iremos aumentar para . Veja que a gente costuma fazer isso utilizando a seguinte formula:
E
Em que:
são os intervalos e a quantidade de retângulos.
Temos duas formulas, uma para quando tomamos o do lado esquerdo do retângulo e outra para quando tomamos o lado direito.
Dito isso, vamos resolver.
Passo 2
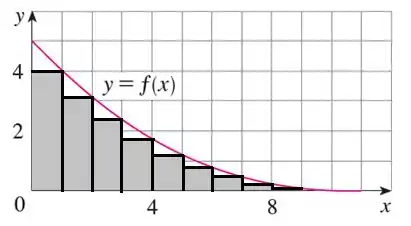
- Vamos lá, vemos na figura que o gráfico de é decrescente, assim vamos encontrar uma estimativa mais baixa usando pontos finais direitos, como vamos usar retângulos temos que , assim:
- Vamos achar agora com , assim:
Temos que:
Aqui nós sabemos que e são os limites de integração, assim:
Vamos calcular o somatório:
Tomando os valores da nossa função nos lados a direita dos nossos retângulos:
Aqui temos o esboço dos retângulos:
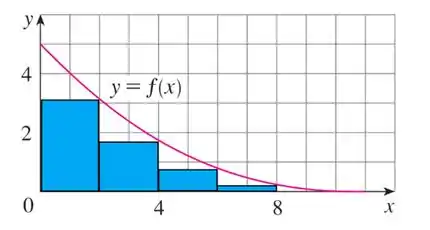
Agora como vemos na figura que o gráfico de é decrescente, vamos encontrar uma estimativa mais alta usando pontos finais esquerdos, como vamos usar retângulos temos que , assim:
Temos que:
Aqui nós sabemos que e são os limites de integração, assim:
Vamos calcular o somatório:
Tomando os valores da nossa função nos lados a esquerda dos nossos retângulos:
Aqui temos o esboço dos retângulos:
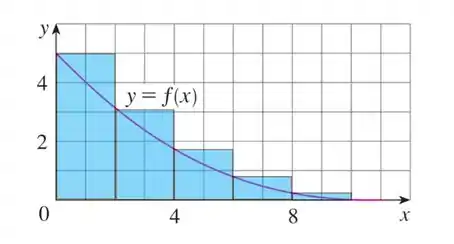
Passo 3
Temos que:
Aqui nós sabemos que e são os limites de integração, assim:
Vamos calcular o somatório:
Tomando os valores da nossa função nos lados a direita dos nossos retângulos:
Aqui temos o esboço dos retângulos:
Passo 3
Vamos calcular o somatório de :
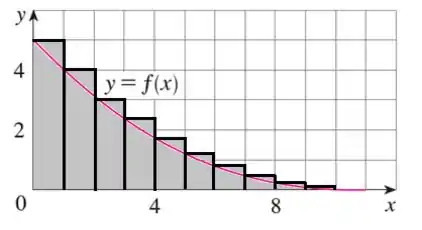
Tomando os valores da nossa função nos lados a esquerda dos nossos retângulos:
Aqui temos o esboço dos retângulos:
Resposta
- e
- e