Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.7 - Ex. 31
O valor exato da integral dada é (confira). Aproxime a integral usando a aproximação pelo ponto médio, a aproximação trapezoidal e a aproximação pela regra de Simpson usando a Fórmula . Dê uma estimativa do erro absoluto e expresse suas respostas com pelo menos quatro casas decimais.
Passo 1
E aíííí, galerinha! Prontos pra mais um exercício com o Responde Aí?
Bom, para esse exercício em questão, a ideia é bem simples. Vamos resolver da maneira mais trivial: apenas calculando a integral aplicando as fórmulas das aproximações citadas.
Assim, temos três métodos. O primeiro deles é dado por aproximação pelo ponto médio:
O outro é a aproximação trapezoidal dada por:
E o último é a regra de Simpson, que iremos usar a fórmula que depende dos resultados das outras duas regras:
Com isso, podemos montar uma tabela para cada valor de nos subintervalos a fim de facilitar o nosso trabalho.
Para esse caso temos os seguintes valores:
Passo 2
Então, montando uma tabela com as informações necessárias para o cálculo das duas primeiras aproximações, iremos ter:
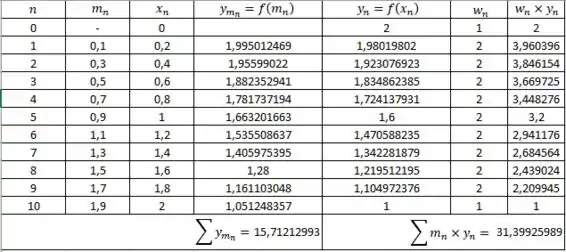
Onde é o ponto médio, é o extremo do intervalo da aproximação trapezoidal e ´o multiplicador de cada termo na aproximação trapezoidal.
Então, a aproximação pelo ponto médio será:
Portanto:
O erro dessa aproximação é dado por:
Então:
Já para a aproximação trapezoidal, teremos o valor de:
Logo:
E o seu erro tem o valor:
Passo 3
Por fim, utilizando a fórmula citada para a regra de Simpson, vamos calcular:
Que resulta em:
E apresenta um erro de: