Para o limite lim x → 1 ⁡ x 3 + x + 1 = 3 , use um gráfico para determinar o valor do δ correspondente a ε = 0,4 .Usando um sistema de computação algébrica para resolver a equação x 3 + x + 1 = 3 + ε , determine o maior valor possível para δ que funcione para qualquer ε0 dado. Tome ε = 0,4 na sua resposta da parte (b) e compare com a sua resposta da parte (a).

δ = 0,093 . δ = x ε - 1 x 0,4 ≈ 1.093272342 e δ = x 0,4 - 1 ≈ 0.093 , o que concorda com a resposta de (a).

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.4 - Ex. 35

Para o limite , use um gráfico para determinar o valor do correspondente a .

Usando um sistema de computação algébrica para resolver a equação , determine o maior valor possível para que funcione para qualquer dado.

Tome na sua resposta da parte (b) e compare com a sua resposta da parte (a).

Passo 1

Eaee, belezinha?? Bom... nessa questão iremos fazer três coisinhas.

Primeiramente queremos determinar o valor de correspondente a para o seguinte limite:

Em seguida, vamos utilizar um software matemático para resolver a seguinte equação de modo que deveremos determinar o maior valor possível para que funcione para qualquer dado:

Por fim, deveremos tomar e comparar com o valor que encontramos de na nossa primeira alternativa.

Para a gente fazer isso, temos que entender a relação sobre esses e .

Bom... a gente os relaciona da seguinte forma:

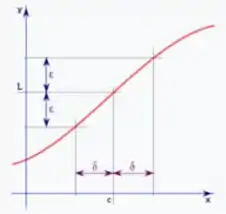
Perceba que sempre que um ponto está dentro de unidades de , está dentro de unidades de .

Agora bora aplicar!! 😉

Passo 2

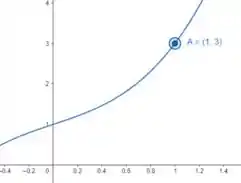
Agora vamos plotar a seguinte função:

Para determinar o valor do correspondente a quando o seguinte limite é satisfeito:

Bom... plotando a função e analisando o limite no ponto , temos:

Agora, vamos calcular os pontos para :

Assim, temos as retas em vermelho que passam por e :

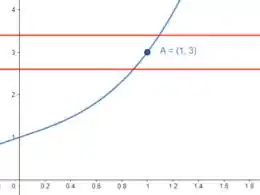
Analisando os pontos de interseção com , obtemos os valores de :

Para temos

Dessa forma, escolhendo um dos pontos, temos que:

Obs: também poderíamos fazer .

Passo 3

Resolvendo a equação através de um software matemático, nós temos duas raízes complexas e uma raiz real que é:

Logo,

Passo 4

Dessa forma, substituindo na equação do passo , iremos obter:

E, calculando :

Que bate com a resposta da letra (a)!!! 😉

Resposta

.
e , o que concorda com a resposta de (a).

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os limites.22.underset(y - 6^-)(lim) (y + 6)/(y^2 - 36)

Encontre os limites.18.underset(x - 2^+)(lim) (x)/(x^2 - 4)

Seja g (t) = {[[t - 2 , t0],[t^2 , 0 = t = 2],[2 t , t2]]) , encontre:(a)underset(t - 0)(lim) g ( t ) (b)underset(t - 1)(lim) g ( t ) (c)underset(t - 2)(lim) g ( t ) .

Seja f (x) = {[[x - 1 , x = 3],[3 x - 7 , x3]]) , encontre:(a)underset(x - 3^-)(lim) f ( x ) (b)underset(x - 3^+)(lim) f ( x ) (c)underset(x - 3)(lim) f ( x ) .

(a) Explique por que o argumento a seguir não está correto. l i m x → 0 + 1 x - 2 x 2 + 2 x = l i m x → 0 + 1 x 1 - 2 x + 2 = ∞ ∙ 0 = 0 (b) Mostre que l i m x → 0 + 1 x - 2 x 2 + 2 x = 1 2 .