Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 4
Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando aumenta.
Passo 1
Falaee, belezinha?? Então... o enunciado nos deu as seguintes equações paramétricas:
No intervalo .
Queremos esboçar a curva que tem as equações paramétricas dadas.
Para fazer isso, vamos criar uma tabelinha de valores que relacionam e, aí poderemos plotar esses pontos no gráfico.
Quando substituirmos os valores de , iremos observar o que acontece com o gráfico quando aumenta e assim vamos indicar a direção, belezinha?? Agora bora lá!! 😉
Passo 2
Assim, quando , por exemplo, teremos:
E
Fazemos o mesmo para os outros valores de e montamos a seguinte tabela:
Show! Agora só precisamos colocar esses pontos em um gráfico e traçar uma linha unindo eles.
Passo 3
Plotando o gráfico, obtemos:
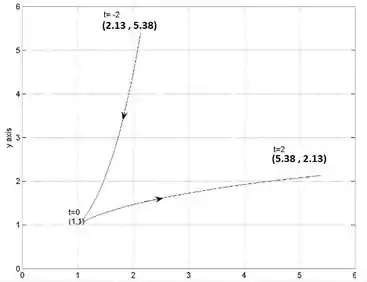
Note que nesse gráfico a gente plotou apenas o intervalo dado no enunciado.
Mas perceba que, para valores de , o valor de tende ao infinito positivo.
Por outro lado, para valores de , o valor de tende ao infinito positivo.
Resposta
