Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 5.3 - Ex. 9e
Uma massa de 100 g é atada a uma mola de constante elástica 0,016 N/cm. Após a massa atingir o equilíbrio, seu suporte oscila de acordo com a fórmula , em que representa o deslocamento a partir da posição de equilíbrio. Vejo o problema 7 e a figura 5.26.
(e) Esboce o gráfico da equação de movimento
Passo 1
Agora o gran finale é esboçar o gráfico da equação de movimento que encontramos lá na letra A, que é:
Bom gente, nos itens anteriores, encontramos que os extremos ocorrem em
E:
E valem
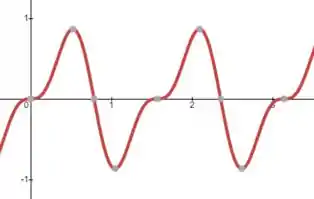
Então nossa curva da soma de duas senoides vai ficar assim:
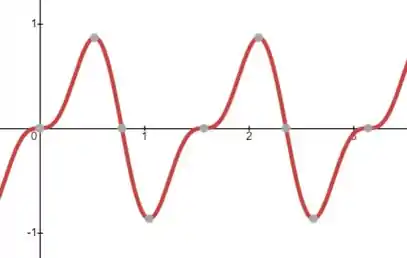
Resposta
Exercícios de Livros Relacionados
Em amortecimento crítico, qualquer aumento do amortecimento resultará em um sistema ________________.
Um peso de 1,5 kg distende uma mola em 2cm. O peso parte de um ponto 25 cm abaixo da posição de equilíbrio com uma velocidade de 1 m / s para cima.Encontre a equação que descreve o movimento harmônico
Na presença de amortecimento, os deslocamentos de um peso em uma mola irão aproximar-se sempre de zero quando t → ∞ . _______________________
O período do movimento harmônico simples de um peso de 8 kg atado a uma mola cuja constante vale 6,25N / m é _____________ segundos.
Se um peso de 10kg distende uma mola em 2,5c m , um peso de 32kg irá distendê-la em _____ cm.