Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.5 - Ex. 6
Modelo econômico. Considere o seguinte modelo econômico: seja o preço de um único item no mercado. Seja a quantidade do item disponível no mercado. são funções do tempo. Se considerarmos o preço e a quantidade como duas espécies que interagem, poderíamos propor o modelo a seguir:
onde são constantes positivas. Justifique e discuta a adequação do modelo.
- Se , encontre os pontos de equilíbrio desse sistema. Se possível, classifique cada ponto de equilíbrio no que diz respeito à sua estabilidade. Se um ponto não puder ser classificado de imediato, dê uma explicação.
- Realize uma análise da estabilidade gráfica para determinar o que ocorrerá com os níveis de à medida que o tempo aumenta.
- Forneça uma interpretação econômica das curvas que determinam os pontos de equilíbrio.
Passo 1
Substituindo os valores das constantes no problema vamos obter
Igualando as derivadas a 0 para obtermos os pontos de equilíbrio vamos ter
O ponto é um ponto de equilíbrio instável e o outro ponto é inconclusivo perto do ponto as trajetórias são periódicas.
Passo 2
Para avaliarmos o que o item nos pede, tomemos o seguinte gráfico
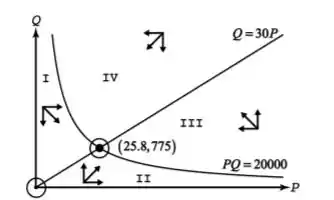
Na região I temos que são maiores que 0, para a região II teremos , já para a região III temos e, por fim, na região IV temos .
Passo 3
A curva pode ser pensada como a curva de demanda enquanto que a curva pode ser vista como a curva de oferta.
Resposta
Ei, a resposta está no passo a passo :)