Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 1.Exercícios de Revisão - Ex. 19
O tanque cônico, mostrado na figura 1.26, derrama água por um orifício no fundo. Se a área da seção transversal do orifício é , encontre a equação diferencial que representa a altura da água em relação ao tempo . Ignore a força de atrito do orifício.
Passo 1
Bom, vamos lá, a gente tem um tanque no formato de um cone e tem água vazando por ele através de um orifício com área de , assim olha:
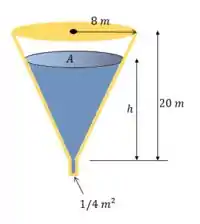
E aí conforme a água vai vazando, a altura da água no tanque vai diminuindo, certo? E nós queremos justamente a equação diferencial que nos dá essa altura em relação ao tempo: queremos , então vamos lá.
Passo 2
Lá no exemplo 8 do seu livro, temos a equação , que fala que a taxa com que o volume de água no tanque decresce (desconsiderando o atrito) é:
Onde é a área do orifício. Mas nós não queremos , queremos , certo?
Então vamos fazer umas manipulações
Passo 3
Dado que o volume de um cone é , temos que o volume de água dentro do tanque no instante pode ser dado por:
Sendo que tanto quanto decrescem com o tempo
Agora vamos pensar em dois triângulos retângulos: o primeiro com catetos e e o outro com catetos e . Por semelhança de triângulos na nossa figura, temos:
Substituindo:
Derivando os dois lados em relação a :
Pela regra da cadeia, temos
Então, temos uma nova expressão para , vamos substituir lá na expressão
Passo 4
Temos
Susbtituindo em :
Belezinha meu povo, agora é só substituir os valores:
Então: