Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.2 - Ex. 1

É mostrado um campo de direções para a equação diferencial y ' = y 1 - 1 4 y 2 .

  1. Esboce os gráficos das soluções que satisfazem as condições iniciais dadas.

    1. y 0 = 1
    2. y 0 = - 1
    3. y 0 = - 3
    4. y 0 = 3

  2. Ache todas as soluções de equilíbrio.

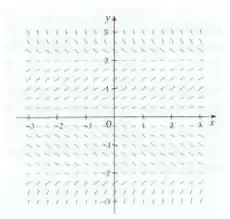
Passo 1

(i) Precisamos esboçar o gráfico no campo vetorial dado que satisfaz a condição inicial de que

y 0 = 1 . Basta pegar o campo, marcar o ponto inicial e fazer o traçado seguindo as setinhas, assim:

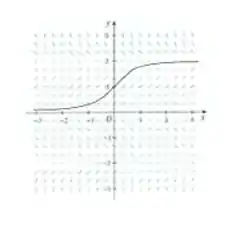
Passo 2

  1. (ii) y 0 = - 1 Podemos desenhar o gráfico da mesma forma como no item anterior:

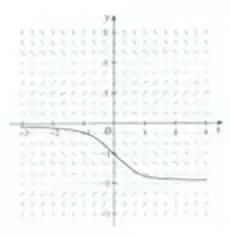
Passo 3

  1. (iii) y 0 = - 3

Passo 4

  1. (iv) y 0 = 3

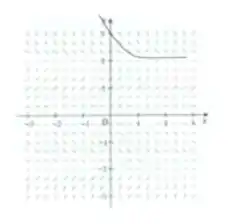
    2. Passo 5

    Podemos unir todos esses gráficos em um só, assim ficamos com ele assim:

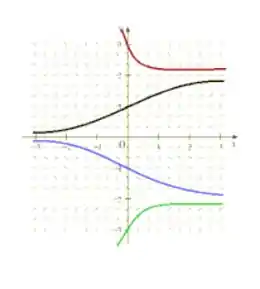
    Passo 6

  2. Agora precisamos encontrar todas as soluções de equilíbrio da equação.

Observando nosso desenho do item (a), percebemos que os vetores nunca se aproximam das linhas horizontais y = 2 , y = 0 , y = - 2 . Então essas são as soluções de equilíbrio.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aplicar os operadores lineares à função s e n (w t) .
D 3 + D 2 + D - 1 às seguintes funções:
Aplicar os operadores lineares à função s e n (w t) .
Aplicar os operadores lineares à função s e n (w t) .
D 3 + D 2 + D - 1 às seguintes funções: