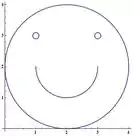
Use uma calculadora gráfica ou um computador para reproduzir a figura.
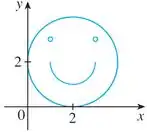
Passo 1
Olha sóóó...Que questão feliz!!! ![]()
Bom.... Vamos separar a nossa figura em 4 partes, indicadas abaixo:
- A circunferenca maior será a parte 1;
- 0 sorriso será a parte 2;
- O olho a esquerda será a parte 3
- O olho a direita sesá a parte 4.
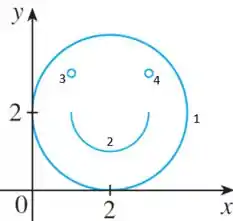
Passo 2
Vamos analisar cada passo desse lindo rostinho feliz.
Na Parte 1 temos uma circunferência centrada em e o raio . A equação geral de um círculo com centro e raio é dada por:
Neste caso, , e , então a equação do círculo é:
Para parametrizar o círculo, podemos usar as coordenadas polares. As coordenadas polares de um ponto na circunferência são dadas por: , onde é o parâmetro.
Substituindo , e , temos:
Essas são as equações paramétricas da circunferência com centro (2,2)(2,2) e raio 22, onde 𝑡t é o parâmetro.
Passo 3
Na parte 2 podemos parametrizar uma semicircunferência com centro e raio no intervalo de a , podemos usar as coordenadas polares. As coordenadas polares de um ponto na semicircunferência são dadas por , onde é o parâmetro.
Dado que o centro é e o raio é , temos , e . Portanto, as equações paramétricas da semicircunferência são:
onde varia de a .
Passo 4
Se os olhos são circunferências com raios de e centros nos pontos e , podemos parametrizá-los usando coordenadas polares.
Para um círculo com centro e raio , as coordenadas polares dos pontos na circunferência são dadas por , onde é o parâmetro.
- Para o olho esquerdo com centro em (1,3) e raio de 0.1, as equações paramétricas são:
- Para o olho direito com centro em e raio de , as equações paramétricas são:
Essas equações representam as coordenadas dos pontos ao longo da circunferência dos olhos, onde é o parâmetro que varia de a . Isso cria a ilusão de círculos perfeitamente desenhados.
Resposta
O gráfico representa um rostinho sorridente com um círculo como rosto, uma semi-circunferência como sorriso e dois pequenos círculos como olhos brilhantes. O rosto tem centro em e raio , o sorriso tem raio e vai de a , enquanto os olhos estão nos pontos e . É uma representação simpática e alegre!
Plotando esses resultados num software “boladão” desses aí ![]()