Esboce um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais, verticais, obliquas e curvilíneas e dê suas equações. Identifique (se houver) os pontos em que o gráfico cruza uma assíntota. Confira seu trabalho com um recurso gráfico.

23.

Antes de calcular o gráfico, vamos achar as assíntotas para ter uma noção melhor de como essa função vai se comportar.

Começando pela assíntota vertical: ela ocorre para pontos não definidos, por exemplo pontos que o denominador zera, no caso da nossa equação o ponto em que , então sabemos que nossa assíntota vertical é nesse ponto e nosso gráfico “explode” nele.

A assíntota horizontal é calculada fazendo o e se a gente tiver um valor constante, esse é o ponto da onde temos a assíntota horizontal

Para resolver esse limite vamos dividir pelo denominador de maior potencia, no caso x

Substituindo por , lembrando que divisão por , dá zero, vamos ter :

Então, como nossa assíntota horizontal não deu um número constante, não temos assíntota horizontal

Como a gente não tem assíntota horizontal, vamos analisar a assíntota oblíqua, que é ninguém mais ninguém menos que uma reta, então tem a forma de , onde e são calculados da seguinte forma:

Vamos então começar com :

Como não temos um número constante, não existe assíntota oblíquoa.

A assíntota curvilínea é o quociente da divisão entre os polinômios de que vai ser a divisão entre os polinômios dividido por , fazendo a divisão entre os polinômios, achamos que o quociente dessa divisão é .

Agora que já temos as assíntotas, vamos fazer um esboço do gráfico.Sabemos que ele explode em -2, de acordo com a assíntota vertical; ele não tem assíntota horizontal mas tem curvilínea, que é a curva .

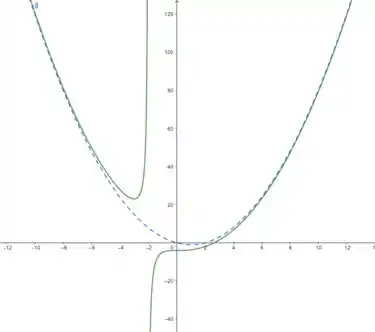
No gráfico, a linha solida verde é nosso gráfico e a linha azul pontilhada a nossa assíntota curvilínea!