Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.4 - Ex. 69
O que é uma área líquida com sinal ? De que forma esse conceito expande nossa aplicação do método do retângulo?
Passo 1
A definição de área líquida com sinal é o seguinte:
“Se a função for contínua em , então a área líquida com sinal entre a curva e o intervalo é definida por:
De forma mais clara um pouquinho: a área líquida com sinal é a diferença da área que está acima de e abaixo da curva e a área que está abaixo e acima de .
Passo 2
Vamos ver um exemplo aqui pra você sacar melhor:
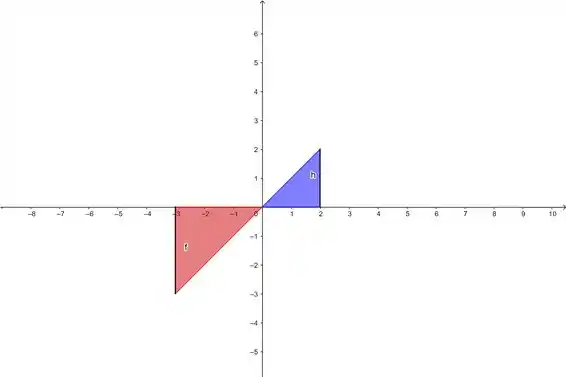
A área líquida aqui é a diferença entre a área azul e a vermelha. Entendeu? Pra baixo é negativo e pra cima é positivo!
E aí dessa forma, usando retângulo para formar as áreas, é só a gente diminuir a área dos retângulos que ficam pra baixo do eixo dos que ficam por cima, e aí está calculada nossa área líquida😉
Resposta
Ei, a resposta está no passo a passo :)