Exercícios de Esboço de Gráfico – Assíntota Oblíqua - Lista de Exercícios Resolvida
Questão 1
Seja .
- Determine todas as assíntotas (horizontais, verticais e oblíquas) de , justificando quando não houver
- Determine os pontos de máximo e mínimo, justificando quando não houver
- Esboce o gráfico da curva acima
Questão 2
Seja .
- Determine todas as assíntotas (horizontais, verticais e oblíquas) de , justificando quando não houver
- Determine os pontos de máximo e mínimo, justificando quando não houver
- Esboce o gráfico da curva acima
Questão 3
Seja ;
- Determine todas as assíntotas (horizontais, verticais e oblíquas) de , justificando quando não houver
- Determine os pontos de máximo e mínimo, justificando quando não houver
- Esboce o gráfico da curva acima
Questão 4
Seja :
Determine todas as assíntotas (verticais, horizontais e oblíquas) justificando quando não houver;
Determine pontos de máximo e mínimo, justificando quando não houver;
Esboce o gráfico de ;
Ver solução completaQuestão 5
Seja . Determine o que se pede justificando a não existência, se for o caso:
- Domínio
- Ponto de interseção do gráfico da função com os eixos cartesianos
- Intervalo de crescimento e decrescimento
- Máximos e mínimos locais
- Assíntotas horizontais, verticais e oblíquas
- Desenhe o gráfico de com todos os elementos encontrados acima
Questão 6
Esboce, no espaço abaixo, o gráfico da função , determinando:
portanto, o gráfico de é:
Ver solução completaQuestão 8
Considere a função :
Determine o domínio de .
Determine os pontos de máximo e mínimo locais de .
Determine todas as assíntotas da curva .
Esboce o gráfico de contemplando todos os elementos obtidos acima.
Ver solução completaQuestão 10
Seja
a) Determine o domínio da função .
b) Determine as equações das retas assíntotas verticais do gráfico de , caso existam.
c) Mostre que a reta é assíntota oblíqua de para a direita (ou seja, quando .
d) Sabendo que é crescente em todo o seu domínio e que a reta é assíntota oblíqua do gráfico de para os dois lados (ou seja, quando e ). Esboce abaixo o gráfico de e suas assíntotas verticais, caso existam.
Ver solução completaQuestão 11
Considere a função dada por
- Determine os intervalos onde cresce, decresce e os pontos de máximo e mínimo locais de .
- Determine os intervalos onde possui concavidade para cima, para baixo e os pontos de inflexão de .
- Calcule os limites pertinentes e discuta a existência de assíntotas.
- Esboce o gráfico de .
Questão 12
Seja . Determine o que se pede justificando a não existência, se for o caso:
- Domínio
- Ponto de interseção do gráfico da função com os eixos cartesianos
- Intervalo de crescimento e decrescimento
- Máximos e mínimos locais
- Assíntotas horizontais, verticais e oblíquas
- Desenhe o gráfico de com todos os elementos encontrados acima
Questão 13
Considere a função definida por
Onde e
- Determine o valor das constantes e para que seja contínua e diferenciavel.
- Atribua às constantes a e b os valores encontrados no item anterior. Determine, caso existam:
- Faça um esboço do gráfico de e de suas assíntotas, caso existam.
b.1) As retas assíntotas horizontais do gráfico de
b.2) As retas assíntotas verticais de .
b.3) As retas assíntotas oblíquas do gráfico de .
b.4) Os intervalos de crrescimento e decrescimento de .
b.5) Os intervalos onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo
Questão 14
Questão 2:
Considere a função definida por
- Determine o domínio da função .
- Determine os intervalos de crescimento e os de decrescimento de , caso existam.
- Determine as equações das retas assíntotas horizontais do gráfico de , caso existam.
- Determine as equações das retas assíntotas verticais do gráfico de , caso existam.
- Determine as equações das retas assíntotas oblíquas do gráfico de , caso existam.
- Sabendo que no intervalo o gráfico de tem concavidade voltada para baixo, e que no intervalo o gráfico de tem concavidade voltada para cima, utilize as informações obtidas nos itens anteriores para esboçar o gráfico de e suas retas assíntotas, caso existam.
Questão 15
Esboce o gráfico de , determinando seu domínio, os intervalos de crescimento e de decrescimento de , concavidades e assíntotas (caso existam).
Ver solução completaQuestão 16
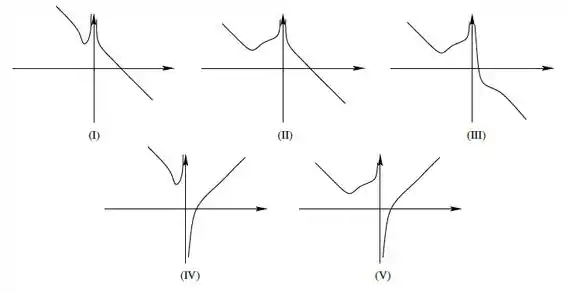
Considere a função dada por:
Assinale a alternativa cujo gráfico mais se assemelha ao gráfico de :
Questão 17
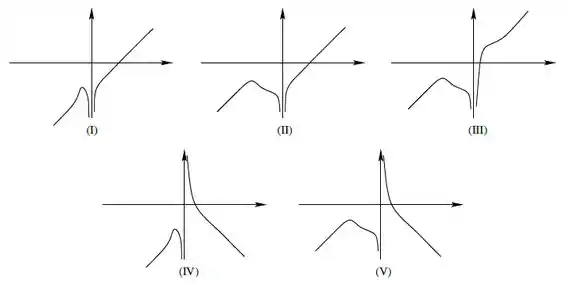
Considere a função dada por:
Assinale a alternativa cujo gráfico mais se assemelha ao gráfico de :
Questão 18
Seja .
(a) Determine os intervalos de crescimento/decrescimento de , e os seus pontos de máximo/mínimo.
(b) Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão.
(c) Caso existam, encontre as assíntotas horizontais e verticais de .
(d) Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c).
Ver solução completaQuestão 19
Para a próxima função:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais;
- Esboce o gráfico, utilizando as informações dos itens anteriores.
Questão 20
Para a seguinte função:
Encontre as assíntotas inclinadas e esboce o gráfico, e para isso:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais e inclinadas;
- Esboce o gráfico, utilizando as informações dos itens anteriores
Questão 21
Para a seguinte função:
Encontre as assíntotas inclinadas e esboce o gráfico, e para isso:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais e inclinadas;
- Esboce o gráfico, utilizando as informações dos itens anteriores
Questão 22
Para a seguinte função:
Encontre as assíntotas inclinadas e esboce o gráfico, e para isso:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais e inclinadas;
- Esboce o gráfico, utilizando as informações dos itens anteriores
Questão 23
Para a próxima função:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais;
- Esboce o gráfico, utilizando as informações dos itens anteriores.
Questão 25
Para a próxima função:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais;
- Esboce o gráfico, utilizando as informações dos itens anteriores.
Questão 26
Seja :
Determine todas as assíntotas (verticais, horizontais e oblíquas) justificando quando não houver;
Determine pontos de máximo e mínimo, justificando quando não houver;
Esboce o gráfico de ;
Ver solução completaQuestão 27
A respeito das seguintes funções
I.
II.
Determine:
a) Domínio;
b) Intersecções com os eixos (explicitar as raízes);
c) Assíntotas, caso existam;
d) Intervalos de crescimento ou decrescimento;
e) Pontos de máximo ou mínio locais e absolutos da função, e os respectivos valores da função nesses pontos;
f) Concavidade e ponto de inflexão;
g) Use as informações dos itens (a-f) para esboçar o gráfico da função.
Ver solução completaQuestão 28
Para a próxima função:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais;
- Esboce o gráfico, utilizando as informações dos itens anteriores.
Questão 29
Para a próxima função:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais;
- Esboce o gráfico, utilizando as informações dos itens anteriores.
Questão 31
Considere a função
Determine, caso existam:
a) as equações das assíntotas horizontais do gráfico de .
b) as equações das assíntotas oblíquas do gráfico de .
c) os intervalos de crescimento e de decrescimento de .
d) Utilizando as informações obtidas nos itens anteriores, esboce o gráfico da função e suas retas assíntotas. Mas em seu desenho as abcissas dos pontos de máximo local e mínimo local do gráfico de , caso existam.
Ver solução completaQuestão 32
Para a próxima função:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais;
- Esboce o gráfico, utilizando as informações dos itens anteriores.
Questão 35
Considere a função e determine o que se pede calculando todos os limites necessários. Caso não haja, justifique por que não há.
OBS.: é a função inversa da função tangente.
Domínio de ;
Derivada de ;
Equação de cada uma das assíntotas verticais da curva ;
Equação de cada uma das assíntotas horizontais da curva ;
Equação de cada uma das assíntotas oblíquas (inclinadas) da curva .
Ver solução completaQuestão 36
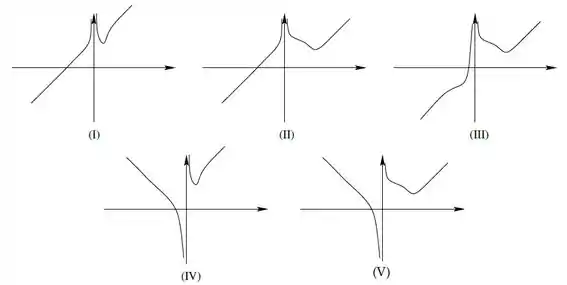
Considere a função dada por:
Assinale a alternativa cujo gráfico mais se assemelha ao gráfico de :
Questão 37
Considere a função
Determine o seu domínio, os intervalos de crescimento e decrescimento, estude e classifique os pontos críticos (se existirem), estude as concavidades e classifique os pontos de inflexão (se existirem), determine as assíntotas (verticais, horizontais e/ou oblíquas), e esboce o gráfico de .
Ver solução completaQuestão 38
Para a próxima função:
- Encontre os intervalos para os quais a função é crescente ou decrescente;
- Encontre os valores de máximo e mínimo locais;
- Encontre os intervalos de concavidade e os pontos de inflexão;
- Encontre as assíntotas horizontais e verticais;
- Esboce o gráfico, utilizando as informações dos itens anteriores.