Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 9.1 - Ex. 6

  1. Mostre que cada membro da família de funções y = ( l n x + C ) / x é uma solução da equação diferencial x 2 y ' + x y = 1 .
  2. Ilustre a parte (a) traçando vários membros da família de soluções na mesma tela.
  3. Encontre a solução da equação diferencial que satisfaça a condição inicial y 1 = 2 .
  4. Encontre a solução da equação diferencial que satisfaça a condição inicial y 2 = 1 .

Passo 1

  1. Bom, vamos começar!

    2. O enunciado fala que temos uma família de soluções possíveis, isso acontece porque temos uma constante ali na nossa expressão. Logo, aquela constante pode assumir diversos valores e ainda assim teríamos uma solução.

    Aqui queremos mostrar que y = ( l n x + C ) / x é solução de x 2 y ' + x y = 1 .  

    E para isso vamos derivar a nossa y e tentar substituir lá na EDO para ver no que vai dar.

    Mas antes precisamos deixar essa EDO com uma cara mais amigável, deixando o y ' em evidência:

    x 2 y ' + x y = 1

    x 2 y ' = 1 - x y

    y ' = 1 - x y x 2

    Passo 2

    Derivando, nós vamos ter:

    y ' = l n x + C x '

    Aqui teremos uma regra do quociente...

    y ' = l n x + C ' . x - l n x + C . x ' ) x 2  

    Derivando l n x + C nós teremos...

    l n x + C ' = 1 x + 0 = 1 x

    E a derivada de x ' ...

    x ' = 1

    Substituindo na nossa regra do quociente, vamos ficar com

    y ' = 1 x . x - l n x + C . 1 x 2

    y ' = 1 - l n x - C x 2

    Agora vamos pegar a nossa EDO

    y ' = 1 - x y x 2

    E substituir nela, tanto o y ' que encontramos e o y que foi dado no enunciado...

    1 - l n x - C x 2 = 1 - x l n x + C x x 2

    1 - l n x + C x 2 = 1 - l n x + C x 2

    Prontinho, provamos a nossa letra a ) !

     

    Passo 2

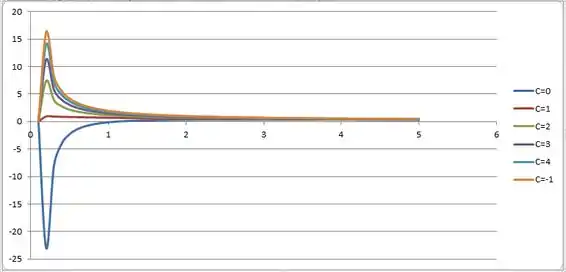
Para resolver essa questão eu usei o famoso Excel e plotei a nossa y no intervalo entre 0 e 5 .

Aqui, usei como constantes os valores de C = 0 ,   1 ,   2 ,   3 ,   4 ,   - 1

Passo 2

Chegou a hora de tirarmos a nossa constante de jogo!

A letra c) pede para a gente encontrar a solução quando tivermos a condição y 1 = 2 .

Como provamos que a nossa y dada no enunciado é uma família de soluções, vamos encontrar a solução para quando tivermos essa condição de contorno, olha só...

A nossa y é uma função de x e é dada por:

y x = ( l n x + C ) / x

Usando a condição de contorno:

y 1 = l n 1 + C 1 = 2

Vamos encontrar nossa constante que ocorre nesse caso, lembrando que l n 1 = 0 ...

0 + C 1 = 2

C = 2

E substituindo na nossa y , vamos encontrar a nossa solução:

y = ( l n x + 2 ) / x

Passo 3

Para fechar com tudo, é só fazermos agora a letra d), que é bem parecida com a letra c), mas o contorno mudou

Agora vamos usar que y 2 = 1

y x = ( l n x + C ) / x

Substituindo o contorno:

y 2 = l n 2 + C 2 = 1

l n 2 + C = 2

C = 2 - l n 2

E por fim, substituindo na nossa y ,   para encontrar a solução!

y = ( l n x + 2 - l n 2 ) / x

Resposta

(c) y = ( l n x + 2 ) / x

(d)

( l n x + 2 - l n 2 ) / x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Equações IntegraisNos Exercícios 7-10, escreva uma equação diferencial equivalente de primeira ordem e condição inicial y .
Equações IntegraisNos Exercícios 7-10, escreva uma equação diferencial equivalente de primeira ordem e condição inicial y .
Equações IntegraisNos Exercícios 7-10, escreva uma equação diferencial equivalente de primeira ordem e condição inicial y .
81.Use a Lei do resfriamento de Newton para determinar a temperatura de um corpo num ambiente onde a temperatura é 40 ° , se 30min atrás a temperatura do corpo era 150 ° e 10min atrás era de 90 ° .
Os psicólogos interessados em teoria do aprendizado estudam as curvas do aprendizado. Uma curva de aprendizado é o gráfico de uma função P ( t ) , o desempenho de alguém aprendendo uma habilidade como