Mostre que a curvatura máxima da curva é , a qual ocorre no ponto .
Passo 1
E aí, pessoal!! Bora pra mais um exercício com o Responde Aí? Vem com a gente :D
Pra começarmos esse exercício, precisamos lembrar do conceito de curvatura e do raio de curvatura. Na seção do livro Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis - 1ª Ed., temos que a curvatura de uma curva é a medida da taxa de variação de sua direção e pode ser dada por:
Quando a curva é plana e possui a forma cartesiana .
Como queremos saber o valor máximo da curvatura, vamos aplicar a propriedade das derivadas para encontrar esse valor. Para tanto, vamos derivar a equação da curvatura e igualar o resultado dessa operação a zero.
Dessa forma, provavelmente teremos uma função polinomial e iremos verificar se o ponto dado pelo enunciado é um ponto crítico.
Por fim, precisamos determinar se o ponto crítico é um ponto de máximo ou mínimo valor dependendo da concavidade da curva na respectiva coordenada.
Passo 2
Dessa forma, para calcularmos a curvatura através da fórmula dada, precisamos determinar a primeira e segunda derivada da função. Então, derivando-a, teremos:
Derivando novamente:
Passo 3
A partir da equação da curvatura dada, temos que:
Assim:
Por conveniência, vamos desenvolver o termo elevado ao cubo e reescrever o termo como :
Pela potenciação, podemos aplicar a seguinte propriedade:
Assim, a curvatura terá a forma:
Então:
Passo 4
Com a equação da curvatura determinada, agora precisamos derivar ela e igualar o resultado a zero. Podemos aplicar a regra do quociente dada por:
Pra fazer essa derivada. Logo:
Isso resulta em:
Passo 5
Partindo pra próxima etapa, temos que igualar esse resultado a zero, tal que:
Multiplicando ambos os lados da equação pelo termo do denominador do lado direito, temos:
Assim:
Multiplicando toda a equação, novamente, por agora:
Como se deseja saber se o ponto é o ponto máximo da curvatura, vamos substituir o valor de do ponto nessa equação dada, tal que o resultado dessa substituição deve ser zero para que o ponto seja crítico.
Com isso, :
Ou seja:
Assim, provamos que o ponto dado é um ponto crítico.
Passo 6
Pela segunda derivada, temos que se o seu valor for maior que zero, a concavidade da função é para cima; caso seja menor que zero, a concavidade é para baixo. Visto que a nossa segunda derivada é dada por:
O seu valor é negativo e, logo, a concavidade é para baixo. Isso significa que o ponto crítico que encontramos é um ponto de máxima curvatura, como podemos ver no esboço a seguir:
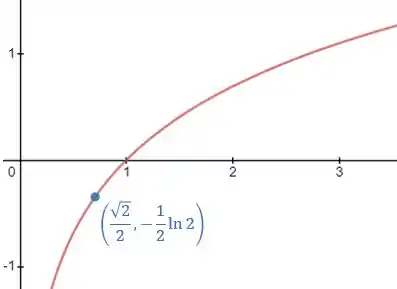
Por fim, para confirmarmos o valor da curvatura, vamos substituir o valor de do ponto na equação da curvatura:
Portanto:
Tirando a raiz quadrada:
Assim, podemos mostrar que a curvatura máxima no ponto tem o valor:
Resposta
Ei, a resposta está no passo a passo :)