Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.9 - Ex. 7
Seja (ver o exemplo ). Mostre que a curvatura é mínima no ponto mais alto da curva, e máxima no ponto mais baixo. Encontre os pontos de velocidade máxima e mínima. Esboce a curva, e os vetores velocidade e aceleração nos pontos mais alto e mais baixo da curva.
Passo 1
E aí, pessoal!! Bora pra mais um exercício com o Responde Aí? Vem com a gente :D
Pra começarmos esse exercício, precisamos lembrar do conceito de curvatura e do raio de curvatura. Na seção do livro Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis - 1ª Ed., o Teorema (página ) dessa seção nos dá uma fórmula mais fácil para o cálculo da curvatura de uma curva e é dada por:
Tal que:
é o vetor velocidade;
é a velocidade escalar;
é o vetor aceleração.
Essas definições se encontram na Seção no item Definição do livro.
Para resolver o numerador, precisamos nos recordar que o produto vetorial entre dois vetores pode ser resolvido através do determinante. Supondo dois vetores e , o produto vetorial entre eles é:
Além disso, para encontrarmos os valores máximo e mínimo, podemos aplicar a propriedade da derivada para encontrar os pontos críticos e, então, determinar qual valor esses pontos têm.
Passo 2
Dessa forma, para calcularmos a curvatura através da fórmula dada, precisamos determinar a primeira e segunda derivada da função dada. Tendo a equação:
Então, derivando-a uma vez, teremos:
E, fazendo isso novamente:
Ainda, a velocidade escalar terá o valor:
Logo:
Se você se lembrar da identidade trigonométrica:
A velocidade escalar pode ser reescrita como:
Ou seja:
Com esses resultados, conseguimos encontrar a forma da curvatura substituindo-as na sua fórmula dada no Passo anterior. Logo, a curvatura pode ser calculada como:
Tal que:
Passo 3
Resolvendo o produto vetorial pelo determinante:
Então:
Reescrevendo esse resultado como:
E usando a identidade trigonométrica mais uma vez:
Na notação vetorial:
Assim:
Passo 4
Por fim, resolvendo o módulo do denominador e transformando a raiz quadrada em expoente:
Portanto, a curvatura da trajetória do cometa será dada por:
Tirando os fatores comuns, teremos:
Então:
Agora, aplicando a propriedade da primeira derivada, iremos encontrar os pontos críticos da curvatura. Logo:
Então:
Agora, igualando esse resultado a zero:
Podemos multiplicar ambos os lados da equação pelo denominador da direita:
Dessa forma:
Para atender a essa condição, o valor de deve ser:
Que são os pontos críticos.
Passo 5
Para os valores e , o valor de é mínimo , ou seja, é a parte mais baixa da curva. Já para , o valor de é máximo , a parte mais alta da curva.
Então, encontrando os valores da curvatura em cada um desses pontos, teremos:
E:
Como o resultado do ponto é menor, então a curvatura é mínima. Já para os outros dois pontos que têm o resultado maior, a curvatura é máxima, teoricamente (pelo fato de que não há como definir uma curvatura infinita).
Passo 6
Agora, para encontrar os pontos máximo e mínimo da velocidade, podemos analisar a equação dessa variável que foi encontrara anteriormente:
Para a velocidade ser máxima, o valor da função cosseno deve ser igual a . Isso irá ocorrer na seguinte condição:
E, para a velocidade ser mínima, a função cosseno deve ser igual a 1:
Então, concluímos que a velocidade terá valor máximo no ponto e valor mínimo nos pontos e .
Passo 7
Usando cada um desses valores de , podemos substituí-los nas equações da velocidade e aceleração vetoriais e representar os vetores obtidos na figura a seguir:
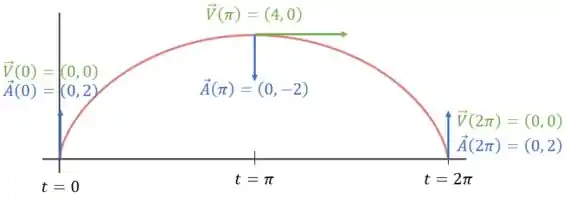
Resposta
A velocidade terá valor máximo no ponto e valor mínimo nos pontos e .