Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.8 - Ex. 35
Mostre que a equação da cônica que tem eixo principal ao longo do semi-eixo e de sua extensão, um foco na origem e cuja diretriz correspondente está abaixo do foco é:
Passo 1
Então galera, essa relação é provada por pura geometria, tudo bem? O problema se torna chatinho para resolver só na montagem, mas depois fica mais tranquilo, você vai ver! Representando a cônica descrita pelo enunciado, teremos:
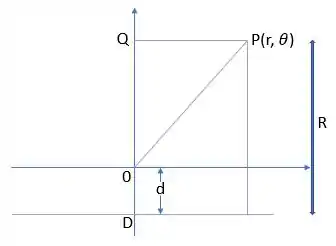
Note que assim como dito pela questão, a diretriz foi representada abaixo do foco, o eixo principal está ao longo do semi-eixo , mas aqui foi representado como qualquer e, por fim, um foco está na origem.
Passo 2
Da figura acima, temos que o ponto só estará presente na cônica se , onde é a excentricidade da cônica em questão. Ademais, como está acima da diretriz , então . Além disso, como , então . Substituindo na expressão que acabamos de escrever incluindo a excentricidade da cônica, teremos:
Mas po, se olharmos na figura, o que seria ? Você deve concordar comigo que podemos escrever essa semirreta da seguinte forma:
Como e , então teremos:
Sendo assim, por fim:
C.Q.D.
Resposta
Ei, a resposta está no passo a passo :)