Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 59

Mostre que a função

f x = x - 6

Não é diferenciável em 6. Encontre uma fórmula para f ' e esboce seu gráfico.

Passo 1

E aí! como vai? 😁

Nesse problema foi dada a função

f x = x - 6

E nosso objetivo é obter f ' x e mostrar que f não é diferenciável em x = 6 .

Tem ideia de como fazemos isso? 😁

Podemos escrever a função da seguinte forma

f x = - x - 6 ,     s e   x - 6 < 0 x - 6 ,     s e   x - 6 ≥ 0

f x = 6 - x ,     s e   x < 6 x - 6 ,     s e   x ≥ 6

Afora para obter a derivada f ' x usamos a equação

f ' x = lim x → a ⁡ f x - f a x - a

Veja só! 😉

Passo 2

Agora, calcularemos o limite da função com x → 6 pela direita e pela esquerda para ver se ele existe e depois a gente calcular a derivada pela definição, daí

lim x → 6 + ⁡ f x - f 6 x - 6

lim x → 6 + ⁡ x - 6 - 0 x - 6

lim x → 6 + ⁡ x - 6 x - 6

lim x → 6 + ⁡ 1 = 1

Agora para uma aproximação pela esquerda, temos

lim x → 6 - ⁡ f x - f 6 x - 6

lim x → 6 - ⁡ x - 6 - 0 x - 6

lim x → 6 - ⁡ 6 - x x - 6

lim x → 6 - ⁡ - x - 6 x - 6

lim x → 6 - ⁡ - 1 = - 1

Então, podemos concluir que

f ' 6 = lim x → 6 ⁡ f x - f 6 x - 6

Não existe, pois os limites laterias existem mas eles não são iguais

Tranquilo até aqui? 👀

Passo 3

Podemos concluir que

f ' x = - 1 ,     s e   x < 6       1 ,     s e   x > 6

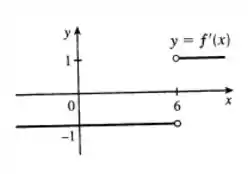
E aí! o que achou? Responde Aí! 😐

Resposta

f ' x = - 1 ,     s e   x < 6       1 ,     s e   x > 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Existe algum valor de c que torne f x = s e n 2 ( 3 x ) x 2 , x ≠ 0 c ,x = 0 Continua em x = 0 ? Justifique sua resposta.