Em quais números a seguinte função é derivável?
Passo 1
Oieee, vamos resolver mais uma comigoo??
Para determinar os números em que a função é diferenciável, precisamos examinar os pontos de descontinuidade e verificar se a função é contínua em cada intervalo.
Para o intervalo
Neste intervalo, a função é que é uma função linear e, portanto, é diferenciável em todos os números reais.
Para o intervalo
Neste intervalo, a função é que é uma função polinomial e, portanto, é diferenciável em todos os números reais.
Para o intervalo :
Neste intervalo, a função é , que é uma função linear e, portanto, é diferenciável em todos os números reais.
Passo 2
Esses são os únicos pontos onde a derivada da função pode não existir devido à descontinuidade da função.
Foi dada a função:
Queremos saber se é derivável.
Aplicamos, então, a derivada expressa pela sua definição pela esquerda e direita de e de
Seja e a derivada pela direita e pela esquerda de 1, respectivamente.
Assim, também, e as derivadas pela direita e pela esquerda de .
Passo 3
Então temos:
Veja que , portanto não é derivável em .
Passo 4
Vamos ver agora para :
Veja que , portanto é derivável em .
Passo 5
Portanto, a função é diferenciável em todos os números reais, exceto em e , onde ocorrem descontinuidades de primeira espécie (descontinuidades de salto), como mostra o gráfico a seguir:
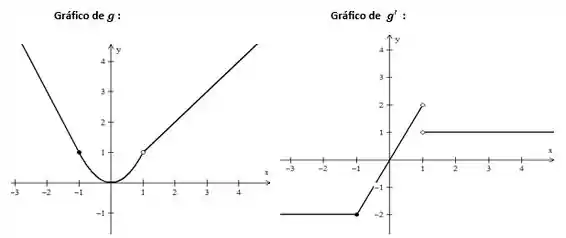
Resposta
não é derivável em 1