Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 50
Mostre que
é contínua e diferenciável em . Esboce o gráfico de na vizinhança de .
Passo 1
Para mostrar que é contínua, devemos satisfazer as seguintes condições:
- está definida
- existe
Vamos ver se satisfaz as três condições.
Passo 2
Com a primeira temos:
Passo 3
Agora com a segunda vamos ver se o limite:
Para calcular esse limite vamos usar Teorema do Confronto, temos que:
Multiplicando tudo por :
Vamos calcular os limites das extremidades das desigualdades, se eles forem iguais, eles forçam o limite do meio ser igual a esse valor:
Assim:
Temos então que o limite existe e é igual a .
Passo 4
O passo anterior nos dá a terceira condição:
Assim a função é contínua.
Passo 5
Vamos agora ver se é diferenciável, vamos calcular o limite:
Agora vamos manipular o limite:
E por último vamos cancelar o termo do numerador e do denominador e vamos aplicar o limite:
Passo 6
Para calcular esse limite vamos usar Teorema do Confronto, temos que:
Multiplicando tudo por :
Vamos calcular os limites das extremidades das desigualdades, se eles forem iguais, eles forçam o limite do meio ser igual a esse valor:
Assim:
Temos então que , assim a função é diferenciável nesse ponto.
Passo 7
O esboço do gráfico de é:
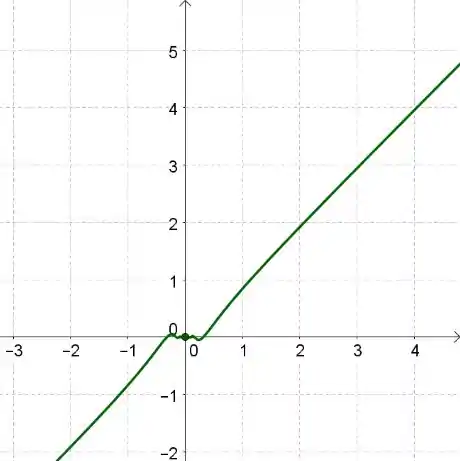
Resposta
