Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.9 - Ex. 37
37. O gráfico de é dado. Estabeleça, explicando, os números nos quais não é diferenciável.
Passo 1
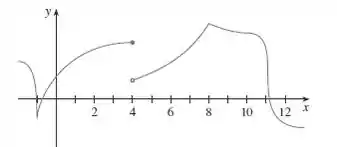
Opa, bora lá! O enunciado nos dá o gráfico:
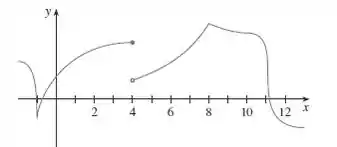
A gente tem que explicar porque a derivada dessa função não existe!
Você lembra quais são os casos em que a derivada não existe?
Só olhando no gráfico!!!
Não se desespere, falarei no próximo passo e deixarei o passo para verificarmos onde não é diferenciável.
Passo 2
Caso, a tangente seja vertical ou a gente tenha um bico ou uma descontinuidade naquele ponto, então a função não será diferenciável.
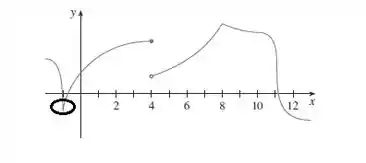
Nesse ponto , não é diferenciável por ter um bico.
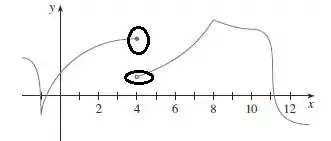
No ponto , a função é descontínua, logo não é diferenciável.
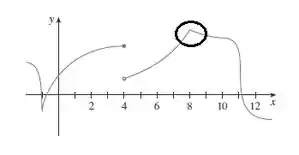
Por conter um bico, a função no ponto não é diferenciável.
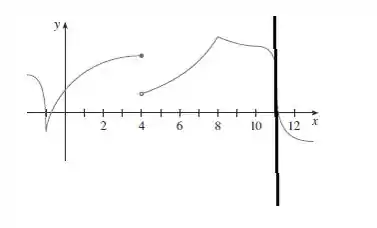
Possui tangente vertical no ponto , então não é diferenciável.
Prontinhoo!
Resposta
, não é diferenciável por ter um bico.
, a função é descontínua, logo não é diferenciável.
Por conter um bico, a função no ponto não é diferenciável.
Possui tangente vertical no ponto , então não é diferenciável.