Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.8 - Ex. 48

Os gráficos de uma função f e sua derivada f ' são mostrando. Qual é maior, f ' ( - 1 ) ou f ' ' ( 1 ) ?

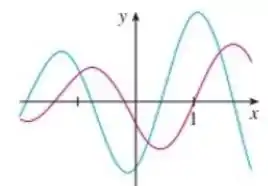
Passo 1

E aí, tudo bem?! Aqui temos as curvas:

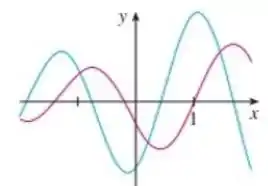
Uma é a derivada f ' x e a outra é a segunda derivada, f ' ' x . O enunciado pergunta quem é maior, f ' ( - 1 ) ou f ' ' ( 1 ) .

Pra a gente descobrir isso temos que lembrar que a derivada de um ponto é a inclinação da reta tangente desse ponto.

Como não temos a curva de f ' ' ( 1 ) vamos precisar olhar pra f ' 1 e pensar em como seria f ' ' 1 e comparar com f ' - 1 .

Mas qual curva é a função e qual é a sua derivada?!

Isso daí a gente vai precisar deduzir!!! Mas calma, vamos lembrar que se a função é crescente a sua reta tangente é crescente, portanto f ' x > 0 e se ela é decrescente f ' x < 0 .

Além disso em um ponto de máximo ou mínimo da função a reta tangente é horizontal. Portanto f ' x = 0 .

Bora colocar a mão na massa?!

Passo 2

Vamos trazer o gráfico pra pertinho:

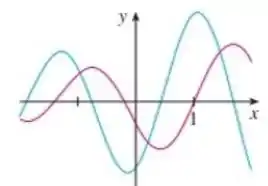
Repara que toda vez que a curva rosa esta em um máximo ou mínimo, a curva rosa toca o eixo x . Ou seja y = 0 ! Maaaas a mesma coisa acontece ao contrário, quando a curva rosa atinge um máximo ou mínimo a curva azul toca o eixo x .

Ou seja, os pontos máximos e mínimos não nos ajudaram em nada nesse caso!

Reparando mais um pouco vemos que sempre que a curva rosa cresce a curva azul é positiva e sempre que ela decresce a curva azul é negativa.

Então a curva rosa é a nossa f x e a azul é f ' ( x ) !

Passo 3

Agora vamos ver quem é maior! f ' ( - 1 ) ou f ' ' ( 1 ) ? Vamos trazer o gráfico pra perto marcando f ' ( - 1 ) e f ' 1 :

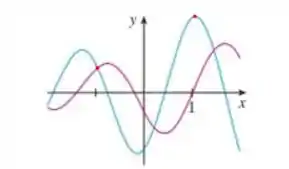
O f ' - 1 é positivo, pra saber seu valor precisaríamos estimar uma escala nesse gráfico. Por enquanto tudo que sabemos é que f ' - 1 > 0 . Vamos segurar essa informação e ver se ela é o suficiente.

Já f ' 1 é um ponto de máximo da curva f ' x , isso significa que a sua derivada, ou seja f ' ' 1 = 0 .

Se f ' ' 1 = 0 e f ' - 1 > 0 , então:

f ' 1 > f ' ' 1

Prontinho!

Resposta

f ' - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

33. Dada f x = x - 1 [ x ] . Faça um esboço do gráfico de f para x e [0,2]. Ache, se existirem: (a) f ´ - 1 ; (b) f ´ + 1 ; (c) f ´ 1 .
37. Na ilustração 1 temos a função valor absoluto definida por f x = x e essa função não é derivável em 0. Prove que f ´ x = x / x para todo x ≠ 0 . (Sugestão: seja x = x 2 .
40. Um fabricante pode obter um lucro de 20 dólares em cada item se até 800 itens forem produzidos por semana. O lucro decresce 0,02 dólares por item acima de 800. (a) Se x itens forem produzidos por
38. Se f x = x e g x = - x , (a) ache uma fórmula para f + g x . (b) Prove que f + g é derivável em 0, embora nem f nem g sejam deriváveis nesse númeroLetra (a)
36. Seja f a função definida por f x = g x - g a x - a , s ex ≠ a g ´ ( a ) , x = a Prove que se g ´ ( a ) existir, f será contínua em a.