Encontre expressões para as funções quadráticas cujos gráficos são mostrados abaixo
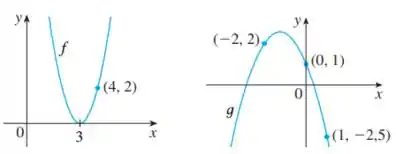
Passo 1
Eaee, belezinha??
Bom... a questão quer que encontremos expressões para os seguintes esboços de funções quadráticas:
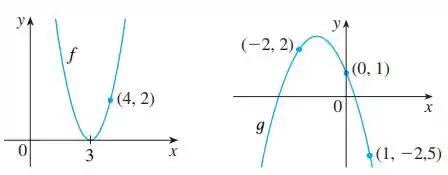
Para isso, vamos analisar uma parábola de cada vez, certinho?
Bora lá!!😉
Passo 2
Para a parábola da esquerda, vemos que seu vértice toca o eixo em apenas um ponto, em .
Nesse sentido, a equação do segundo grau tem a seguinte forma:
A questão ainda nos deu o ponto . Assim, podemos descobrir o valor de :
Assim, a equação do segundo grau que representa a primeira parábola é dada por:
Tranquilo até aqui? 😁
Passo 3
Já na segunda parábola, vemos que ela intercepta o eixo em . Assim temos a equação do segundo grau da seguinte forma:
A figura ainda nos mostra dois pontos aleatórios da parábola: e .
Com esses dois pontos, podemos substituir na equação acima e teremos um sisteminha de equações, onde poderemos descobrir os valores de e .
Bora lá! 😉
Passo 4
Para o ponto :
Para o ponto :
Assim, temos o seguinte sistema de equações:
Resolvendo o sistema, encontramos e .
Assim, temos a nossa equação do segundo grau que descreve a segunda parábola:
Entendeu direitinho?? Responde Aí! 😉
