Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.6 - Ex. 10
Obtenha os gráficos de que revelem todos os aspectos importantes da curva. Estime os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão, e use o calculo para achar essas quantidades exatamente.
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é plotar os gráficos de e para determinar os intervalos de crescimento e decrescimento, os valores extremos, os pontos de inflexão e os intervalos de concavidade.
Parece complicado?
A partir do gráfico de podemos obter os pontos críticos, quando , e os intervalos de inclinação de ... quando a inclinação de é crescente e quando a inclinação de é decrescente.
A partir do gráfico de podemos obter os intervalos de concavidade... quando a concavidade de é para cima e quando a concavidade de é para baixo. Além disso, os pontos de inflexão são obtidos quando temos .
Para determinar os pontos extremos, pegamos os pontos críticos e aplicamos em , se no ponto , significa que o ponto é de mínimo e se o ponto é de máximo.
Sacou? Bora começar!
Passo 2
Vamos começar calculando as derivadas de ...
Como é uma fração de funções de , vamos aplicar a regra do quociente.
Agora vamos aproveitar para calcular a segunda derivada pelo mesmo método...
Tranquilo até aqui?
Passo 3
Agora vamos começar nossas análises...
Vamos usar uma ferramenta gráfica para plotar ...
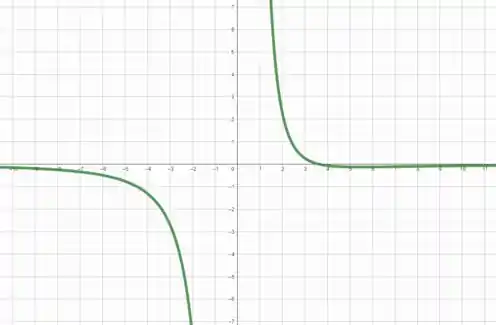
Como discutimos no passo 1, quando temos pontos críticos que podem ser pontos extremos...
Nesse caso vemos que apenas em cruza o eixo , então esse é o único ponto crítico de .
Outra coisa que podemos observar é que quando a função é decrescente, ou seja, quando e quando . Já quando a função , logo, é crescente...
Show?
Passo 4
Agora vamos plotar o gráfico e ...
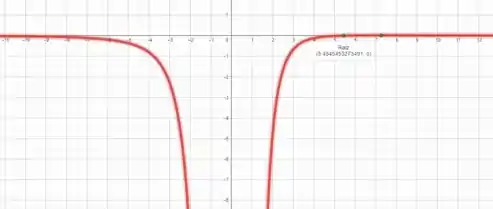
Aqui podemos concluir que quando a função possui concavidade voltada para baixo, ou seja, isso ocorre em e para a função possui concavidade voltada para cima.
cruza o eixo em como vemos no gráfico, então aqui temos um ponto de inflexão.
No passo anterior vimos que em temos um ponto crítico e aqui vemos que nesse ponto , logo, é um ponto de máximo de .
Maravilha!
Passo 5
Por fim, vamos plotar o gráfico de para conferir os dados que acabamos de encontrar.
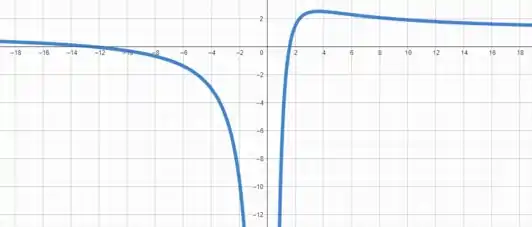
Confirmando os quesitos discutidos nos passos anteriores, vemos que possui concavidade para baixo em e para cima em e em temos um ponto de inflexão já que é o ponto onde a concavidade muda.
Além disso em temos um ponto máximo e quando e a função é decrescente e em a função é crescente.
E aí! o que achou? Responde Aí!
Resposta
possui concavidade para baixo em e para cima em e em temos um ponto de inflexão já que é o ponto onde a concavidade muda.
Além disso em temos um ponto máximo e quando e a função é decrescente e em a função é crescente.