Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.6 - Ex. 1

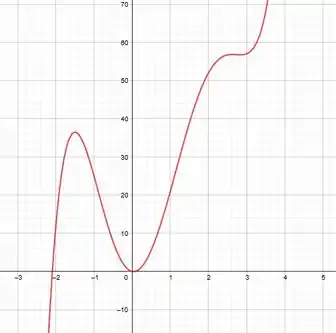
  1. Faça gráficos de f que revelem todos os aspectos importantes da curva. Em particular, você deve usar os gráficos de f ' e f ' ' para estimar os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão.

f x = x 5 - 5 x 4 - x 3 + 28 x 2 - 2 x

Passo 1

E aí blz? Bora pra mais uma questão?

Basicamente vamos ter que calcular a primeira e a segunda derivada e interpretá-las junto com gráfico.

O gráfico de f ’ ( x ) nos dará informações sobre os intervalos de crescimento e decrescimento de f ( x ) . Para isso, precisamos encontrar a derivada de f ( x ) e identificar os pontos críticos (onde f ’ x = 0 ou é indefinida).

O gráfico de f ' ' ( x ) nos ajudará a determinar os intervalos de concavidade e os pontos de inflexão de f ’ ( x ) . Encontre a segunda derivada de f ’ ( x ) e localize onde f ' ' x = 0 ou é indefinida.

Vamos nessa? ☺

Passo 2

Para fazer os gráficos precisamos das funções, assim primeiro vamos derivar f e logo em seguida esboçar os respectivos gráficos de f ,   f ' e   f ' ' .Temos então que:

f = x 5 - 5 x 4 - x 3 + 28 x 2 - 2 x

Usando a regra da potência:

f x = x n → f ' x = n x n - 1

f ' x = 5 x 4 - 20 x 3 - 3 x 2 + 56 x - 2

Onde o gráfico de f ' ( x ) é dado por:

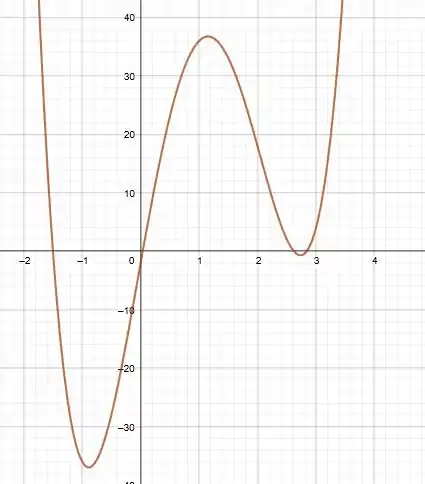
Agora vamos ver onde temos os pontos críticos, ou seja, onde as derivadas são iguais a zero. Para isso é só olhar o gráfico, o ponto mais acima das montanhas e os pontos mais abaixo dos vales, são eles que estamos procurando.

Temos que f ' x é positiva, ou seja está acima do eixo x , nos seguintes intervalos

- ∞ ,   - 1,5 , 0 ;   2,5 , 2,8 ;   ∞ , podemos expressar isso dessa forma em matematiquês:

- ∞ ,   - 1,5 ∪ 0 ;   2,5 ∪ 2,8 ;   ∞

E negativa (abaixo do eixo x ), nos intervalos:

- 1,5 ,   0 ∪ 2,3 ,   2,8

Repare que de 2,3 ,   2,8 temos só um pedacinho abaixo do gráfico.

Esses intervalos são os mesmos de crescimento e de decrescimento respectivamente.

Passo 3

Os pontos de inflexão são dados pelas raízes de f ' ' x , então vamos calculá-la essa derivada:

f ' x = 5 x 4 - 20 x 3 - 3 x 2 + 56 x - 2

Aplicando novamente a regra da potência:

f ' ' x = 20 x 3 - 60 x 2 - 6 x + 56

E agora vamos procurar os valores para os quais f ' ' x = 0 .

No final teremos esses pontos, que serão nossos pontos de inflexões, ou seja, são os pontos que nossa função muda de direção.

P I = - 0,9 ; 0 ,   1,1 ; 0 ,   2,8 ; 0

E o gráfico de f ' ' ( x ) , é dado por:

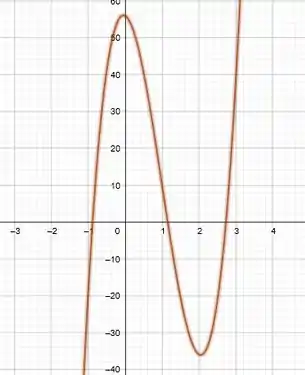
E os intervalos aproximados onde ela é positiva (acima do eixo y ) é dado por:

- 0,9 ,   1,1 ∪ 2,8 ,   ∞

E onde ela é negativa (abaixo do eixo x )

- ∞ ,   - 0,9 ∪ 1,1 ;   2,8

E esses intervalos correspondem às áreas de concavidade para cima ou para baixo, respectivamente.

Passo 4

Vamos interpretar as informações e usar os gráficos de f ’ e f ’ ’ para esboçar o gráfico de (f(x)).

Gráfico de f ( x ) :

  1. Encontramos a derivada de f ( x ) como f ’ ( x ) = 5 x 4 - 20 x 3 - 3 x 2 + 56 x - 2 .
  • Identificamos os intervalos de crescimento e decrescimento:

f ’ ( x ) é positiva nos intervalos ( - ∞ ,   - 1.5 )   ∪   ( 0 ;   2,5 )   ∪   ( 2,8 ;   ∞ ) .

f ’ ( x ) é negativa nos intervalos ( - 1,5 ;   0 )   ∪   ( 2,3 ;   2,8 ) .

  • Pontos de inflexão ( P I ) :
    • Calculamos a segunda derivada de f(x) como f ’ ’ x = 20 x 3 - 60 x 2 - 6 x + 56 .

    Encontramos os pontos onde f ’ ’ ( x )   =   0 :

    P I :   ( - 0,9 ;   0 ) ,   ( 1,1 ; 0 ) ,   ( 2,8 ; 0 ) .

  • Gráfico de f ’ ’ ( x ) :
    • O gráfico de f ’ ’ ( x ) nos ajuda a determinar os intervalos de concavidade.

    f ’ ’ x é positiva (feliz) nos intervalos ( - 0,9 ;   1,1 )   ∪   ( 2,8 ;   ∞ ) .

    f ’ ’ x é negativa (triste) nos intervalos ( - ∞ ;   - 0,9 )   ∪   ( 1,1 ;   2,8 ) .

    Agora, combinando essas informações, como um grande megazord, podemos esboçar o gráfico de f ( x ) . Lembre-se de que os pontos críticos e de inflexão afetam a forma da curva. 😊

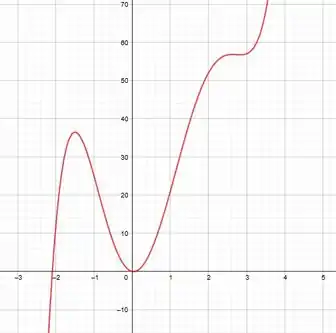
    Resposta

    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    Descreva a mudança no gráfico de f à medida que c varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve imaginar como os pontos de
    A função f x = sen ⁡ x + sen ⁡ 2 x , 0 ≤ x ≤ π , aparece em aplicações a síntese de modulação de frequência (FM).Use uma calculadora gráfica para esboçar um gráfico da f e use esse gráfico para dar um
    Um cabo flexível pendurado sempre tem a forma de uma catenária y = c + a c o s h c o s hx a , em que c e a são constantes e a0 (veja a Figura 4 e o Exercício 52 ). Faça o gráfico de vários membros da
    Esboçe o gráfico de f x = 6 - x começando pelo gráfico de y = x e usando as transformações da Seção 1.3 .Use o gráfico da parte (a) para esboçar o gráfico de f ' .Use a definição de derivada para enco
    Use o método de Newton com a aproximação inicial x 1 = 1 para achar x 2 , a segunda aproximação da raiz da equação x 4 - x - 1 = 0 . Faça o gráfico da função e da reta tangente no ponto 1 , - 1 . Usan