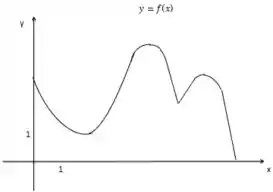
Use o gráfico para estabelecer os valores de máximo e mínimo locais e absolutos da função.
Passo 1
Primeiro, precisamos entender o que é um valor de máximo e mínimo locais e absolutos. É o seguinte: um valor máximo absoluto é quando um número é maior que . Da mesma forma, um valor mínimo absoluto é quando é menor que . Belezinha??
Para o valor de máximo local, temos que para todo em um intervalo aberto contendo . Assim, o valor de mínimo local é quando quando estiver próximo de . Okay? Okay!
Vamos lá resolver!!
Passo 2
Pela nossa explicação, o maior ponto para o valor máximo absoluto é quando e o valor mínimo absoluto, menor ponto, é . Certo?!
Agora os valores dos máximos locais seriam e . Enquanto os valores de mínimo local, são e .
Tranquilo, né?
Resposta
O valor máximo absoluto é quando e o valor mínimo absoluto, menor ponto, é . Agora os valores dos máximos locais seriam e . Enquanto os valores de mínimo local, são e .