Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.1 - Ex. 14a
(i) Dê um palpite sobre o limite (se existir) calculando a função nos pontos especificados.
(ii) Confirme suas conclusões sobre o limite desenhando o gráfico da função sobre um intervalo adequado.
(iii) Use um CAS para encontrar o limite. [Nota: Para as funções trigonométricas, assegure-se de que a calculadora esteja no modo radianos].
(a) ;
(b) ;
(c) ;
Passo 1
(a)Primeiro, calculamos cada função nos pontos especificados. Podemos usar uma calculadora, ou mesmo o Excel. Assim, pra , temos, respectivamente:
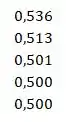
Passo 2
Pra essa função, temos o seguinte gráfico:
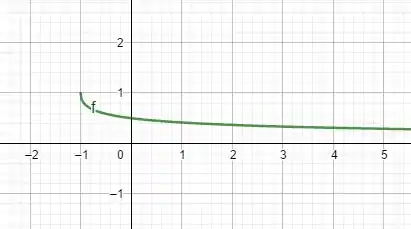
Passo 3
Agora, calculamos o limite e verificamos no gráfico se o que foi calculado é coerente. Pra esse limite, podemos facilmente usar a regra de l’Hopital:
De fato, ao observarmos o gráfico, é possível ver que a função se aproxima de , assim como o resultado da função, calculado nos pontos mais próximos de .
Resposta
Ei, a resposta está no passo a passo :)